[科普中国]-局部时

局部时是布朗运动在点邻域所渡过的时间总量的量度。

简介局部时是布朗运动在点邻域所渡过的时间总量的量度，如果存在极限

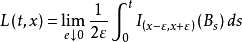
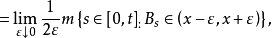
其中 m 为勒贝格测度，则称函数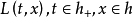 为布朗运动 {Bt} 在 x 除的局部，可以证明，上述极限在 L2 意义下和 a.s. 意义下都是存在的，且 L(t,x) 可定义为 (t,x) 二元连续函数。1

布朗运动（Brownian movement）

布朗运动是微小粒子表现出的无规则运动。1827年英国植物学家R.布朗在花粉颗粒的水溶液中观察到花粉不停顿的无规则运动。进一步实验证实，不仅花粉颗粒，其他悬浮在流体中的微粒也表现出这种无规则运动，如悬浮在空气中的尘埃。后人就把这种微粒的运动称之为布朗运动。以悬浮在水中的藤黄颗粒为例，一个半径为2x10^-7米的藤黄颗粒，质量约为3x10^-17千克，在27℃时它的运动速率接近0.02米/秒。起初人们不了解这种运动的起因。1877年J.德耳索首先指出布朗动是由于颗粒受到液体分子碰撞的不平衡力作用而引起的。随后，1904年法国科学家H.潘卡雷进一步解释，大物体（如线度为0.1毫米）将从各个方面受到运动原子的冲击，打击非常频繁，概率定律使之互相补偿，故它们不移动。微小的粒子受到的打击太少，以至无法补偿。这就是说，布朗运动是液体分子处于不停顿无规则热运动的宏观表现。1905-1906年A.爱因斯坦和M.von斯莫卢霍夫斯基分别发表了理论上分析布朗运动的文章。1908年皮兰用实验验证了爱因斯坦的理论，从而使分子动理论的物理图像为人们广泛接受。

勒贝格测度勒贝格测度是赋予欧几里得空间的子集一个长度、面积、或者体积的标准方法。它广泛应用于实分析，特别是用于定义勒贝格积分。可以赋予一个体积的集合被称为勒贝格可测；勒贝格可测集A的体积或者说测度记作λ(A)。一个值为∞的勒贝格测度是可能的，但是即使如此，在假设选择公理成立时，R的所有子集也不都是勒贝格可测的。不可测集的“奇特”行为导致了巴拿赫-塔斯基悖论这样的命题，它是选择公理的一个结果。

本词条内容贡献者为:

孙和军 - 副教授 - 南京理工大学