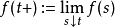
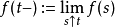 令
令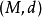 为度量空间,并令
为度量空间,并令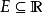 。函数
。函数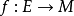 称为右连左极函数。若对于每一
称为右连左极函数。若对于每一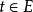 ,都有左极限存在;且右极限存在并等于
,都有左极限存在;且右极限存在并等于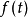 ,即
,即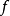 是右连续的且有左极限。1
是右连续的且有左极限。1
全部连续函数都是右连左极函数。
由累积分布函数的定义知所有的累积分布函数都是右连左极函数。
累积分布函数累积分布函数,又叫分布函数,是概率密度函数的积分,能完整描述一个实随机变量X的概率分布。一般以大写“CDF”(CumulativeDistributionFunction)标记。
对于所有实数x ,累积分布函数定义如下:
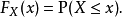
从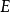 到
到 的所有右连左极函数的集合常记为
的所有右连左极函数的集合常记为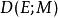 或简记为
或简记为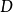 ,称为斯科罗霍德空间,是以乌克兰数学家阿纳托利·斯科罗霍德(Anatoliy Skorokhod)的名字命名。斯科罗霍德空间可以被指派一个拓扑,这一拓扑直觉上能使我们“稍微蠕动空间和时间”(而传统的一致收敛拓扑仅允许我们“稍微蠕动空间”)。为了简化说明,取
,称为斯科罗霍德空间,是以乌克兰数学家阿纳托利·斯科罗霍德(Anatoliy Skorokhod)的名字命名。斯科罗霍德空间可以被指派一个拓扑,这一拓扑直觉上能使我们“稍微蠕动空间和时间”(而传统的一致收敛拓扑仅允许我们“稍微蠕动空间”)。为了简化说明,取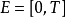 ,
,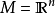 (Billingsley的书中描述了更一般的拓扑)
(Billingsley的书中描述了更一般的拓扑)
首先我们必须定义连续性模的一个模拟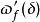 。对于任意
。对于任意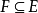 ,使
,使
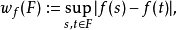 且对于
且对于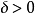 ,将右连左极函数模(càdlàg modulus)定义为
,将右连左极函数模(càdlàg modulus)定义为
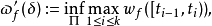
其中最大下界对所有划分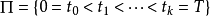 ,
,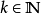 都存在,且
都存在,且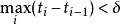 。这一定义对于非右连左极函数
。这一定义对于非右连左极函数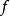 是有意义的(就如通常的连续性模对于不连续函数是有意义的)且可以说明
是有意义的(就如通常的连续性模对于不连续函数是有意义的)且可以说明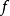 是右连左极函数当且仅当
是右连左极函数当且仅当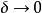 时
时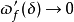 。
。
这是令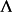 表示从
表示从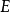 到自身的所有严格递减的连续双射函数的集合(这些函数是“对时间的蠕动”)。令
到自身的所有严格递减的连续双射函数的集合(这些函数是“对时间的蠕动”)。令
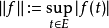 表示
表示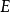 上的函数的一致范数。将
上的函数的一致范数。将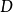 上的斯科罗霍德度量(Skorokhod metric)
上的斯科罗霍德度量(Skorokhod metric)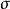 定义为
定义为
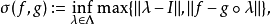 其中
其中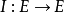 是恒等函数。以“蠕动”这种直观感觉来看,
是恒等函数。以“蠕动”这种直观感觉来看,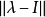 度量了“时间的蠕动”,而
度量了“时间的蠕动”,而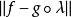 度量了“空间的蠕动”。
度量了“空间的蠕动”。
可以证明斯科罗霍德度量度量的确是度量。由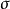 生成的拓扑
生成的拓扑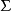 称为
称为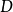 上的斯科罗霍德拓扑(Skorokhod topology)。1
上的斯科罗霍德拓扑(Skorokhod topology)。1
E上的连续函数空间C是D的一个子空间。相对应于C斯科罗霍德拓扑与这里所述的一致拓扑相一致。
完备性虽然D不是关于斯科罗霍德度量σ的一个完备空间,但是可以证明存在具完备性的关于D的拓扑等价度量σ0。
分离性关于σ或σ0的D是可分空间,因此斯科罗霍德空间是Polish空间。
斯科罗霍德空间中的胎紧性通过应用阿尔泽拉-阿斯科利定理,我们可以证明斯科罗霍德空间D上概率测度的一个序列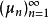 是胎紧的当且仅当同时满足下列两个条件:
是胎紧的当且仅当同时满足下列两个条件:
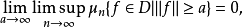 和
和
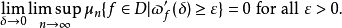
在斯科罗霍德拓扑和函数的逐点加法下,D不是一个拓扑群。2




 扫码下载APP
扫码下载APP

 科普中国APP
科普中国APP
 科普中国
科普中国
 科普中国
科普中国