人物简介
约翰·彼得·古斯塔夫·勒热纳·狄利克雷(Johann Peter Gustav Lejeune Dirichlet,勒热纳·狄利克雷是姓,1805年2月13日-1859年5月5日),德国数学家。他是解析数论的奠基者,也是现代函数概念的定义者。
狄利克雷16岁通过中学毕业考试后,父母希望他攻读法律,但他已选定数学为其终身职业。当时的德国数学界,除高斯一人名噪欧洲外,普遍水平较低;又因高斯不喜好教学,于是狄利克雷决定到数学中心巴黎上大学,那里有一批灿如明星的数学家,诸如P.S.拉普拉斯(Laplace)、A.勒让德(Legendre)、J.傅里叶(Fourier)、S.泊松(Poisson)、S.拉克鲁瓦(Lacroix)、J.B.比奥(Biot)等等。
1822年5月,狄利克雷到达巴黎,选定在法兰西学院和巴黎理学院攻读;其间因患轻度天花影响了听课,幸好时间不长。1823年夏,他被选中担任M.法伊(Fay)将军的孩子们的家庭教师。法伊是拿破仑时代的英雄,时任国民议会反对派的领袖。狄利克雷担任此职,不仅收入颇丰,而且受到视如家人的善待,还结识了许多法国知识界的名流。其中,他对数学家傅里叶尤为尊敬,受其在三角级数和数学物理方面工作的影响颇深。另一方面,狄利克雷从未放弃对高斯1801年出版的数论名著《算术研究》(Dispui-sitiones arithmeticae)的钻研。据传他即使在旅途中也总是随身携带此书,形影不离。当时还没有其他数学家能完全理解高斯的这部书,狄利克雷是第一位真正掌握其精髓的人。可以说,高斯和傅里叶是对狄利克雷学术研究影响最大的两位数学前辈。
1825年,狄利克雷向法国科学院提交他的第一篇数学论文,题为“某些五次不定方程的不可解”(Mémoire sur L'impossibilite de quelques équations indéterminées du cinquieme degré)。他利用代数数论方法讨论形如x5+y5=A·z5的方程。几周后,勒让德利用该文中的方法证明了
当n=5时无整数解;狄利克雷本人不久也独立证明出同一结论。(后来狄利克雷再次研究费马大定理时,证明n=14时该方程无整数解。)
发展历史由于狄利克雷的积分是从下面界定的,所以保证了最小的存在。 这个最终的实现是由黎曼(创造了狄利克雷的原则)和其他人所理解的,直到Weierstrass给出了一个功能达不到最小值的例子。希尔伯特后来证明了黎曼利用狄里克雷的原则。1
狄利克雷原理最早出现在英国数学家格林关于位势理论的著作中,稍后又为高斯和狄利克雷独立提出。狄利克雷在一次讲演中,对函数本身及其诸偏导数都连续的函数类的狄利克雷原理,给出十分确切和完全的叙述,并在1876年由他的一个学生发表。黎曼首先以狄利克雷的名字命名这一原理并应用于复变函数,从而使其得到广泛的关注。然而狄利克雷给出的证明是不完善的。1870年,外尔斯特拉斯以其特有的严格化精神批评了狄利克雷原理在逻辑上的缺陷。他指出:连续函数的下界存在且可达到,但此性质不能随意推广到自变量本身为函数的情形,即在给定边界条件下使积分极小化的函数未必存在。他的非议迫使数学家们放弃狄利克雷原理,但事实上数学物理中的许多结果都依赖于此原理而建立。
在19世纪末20世纪初,希尔伯特采取完全不同的思路来处理这一难题。他通过边界条件的光滑化来保证极小函数的存在,从而恢复了狄利克雷原理的功效。他的工作不仅“挽救”了有广泛应用价值的狄利克雷原理,也丰富了变分法的经典理论。2
狄利克雷原理的进一步发展由原苏联数学家索伯列夫完成,他对于多重调和方程,包括区域的边界由不同维数流形组成的情形进行了叙述,并证明了狄利克雷原理的正确性。
公式表述狄利克雷原理是指将拉普拉斯方程狄利克雷问题化为变分问题的方法。使:
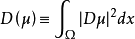 在函数类
在函数类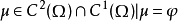 在
在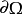 上,
上,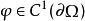 中达到极小的极值函数
中达到极小的极值函数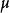 就是拉普拉斯方程狄利克雷问题:
就是拉普拉斯方程狄利克雷问题:
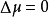
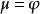
的解。因此,求解拉普拉斯方程狄利克雷问题可化成变分问题,这就是狄利克雷原理。积分D(u)称为狄利克雷积分。
狄利克雷原理告诉我们,如果函数u(x)是泊松方程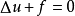 在定义域R上满足边界条件:
在定义域R上满足边界条件: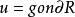 的解,那么u是狄利克雷能量的最小值:
的解,那么u是狄利克雷能量的最小值:
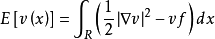 在v中,v = g在的所有两个可微分的函数中(前提是至少存在一个使Dirichlet积分有限的函数)。这个概念以德国数学家彼得·古斯塔夫·勒杰(Dijichlet)命名。3
在v中,v = g在的所有两个可微分的函数中(前提是至少存在一个使Dirichlet积分有限的函数)。这个概念以德国数学家彼得·古斯塔夫·勒杰(Dijichlet)命名。3
组合数学中的抽屉原理抽屉原理又叫鸽笼原理,它是组合数学中判断存在性的一个重要原理。抽屉原理最先由德国数学家狄利克雷运用于解决数学问题,所以也称之为狄利克雷原理。抽屉原理的表述虽然比较简单,很容易理解,但因其变化多,应用广,常常被用于解答各级数学竞赛题。利用抽屉原理,可以作出许多有趣的推理和判断。
抽屉原理的表述:
抽屉原理I:把n+1个苹果放到n个抽屉里,则至少有一个抽屉中有2个或2个以上的苹果。
抽屉原理II:把mxn+r个苹果放到n个抽屉里,则至少有一个抽屉中有不少于m+l个苹果。
当m=l、r=l时抽屉原理II就变为抽屉原理I,因此抽屉原理I是抽屉原理II的特例。
抽屉原理的特点是物体多、抽屉少,而物体个数比抽屉个数多1是利用抽屉原理解题时最常见的情况。抽屉原理用反证法很容易给出证明。
在解决实际问题时,经常利用抽屉原理的另一种提法来探索数量关系。
变形I:在n个抽屉中放入k个苹果,要至少在一个抽屉中有不少于2个苹果,则k的最小值是n+l,即至少需n+l个苹果。
变形II:在n个抽屉中放入k个苹果,要至少在一个抽屉中有不少于m+l个苹果,则k的最小值是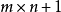 mx:,+l,即至少需
mx:,+l,即至少需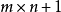 个苹果。4
个苹果。4




 扫码下载APP
扫码下载APP

 科普中国APP
科普中国APP
 科普中国
科普中国
 科普中国
科普中国