[科普中国]-高斯信源嫡

高斯信源熵(entropy of Gauss source)是高斯信源的一种量度。高斯信源是指信源输出的一维随机变量X的概率密度分布是正态分布。

概念高斯信源熵(entropy of Gauss source)是高斯信源的一种量度。高斯信源是指信源输出的一维随机变量X的概率密度分布是正态分布，即：

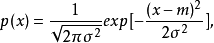式中m是X的均值，σ2是X的方差。这种连续信源称为高斯信源。高斯信源的熵为：

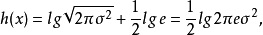式中：

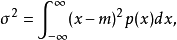当m=0时，X的方差σ2等于信源输出的平均功率。

信源信息科学中最基本、最重要的概念之一。是信息的产生与发出者，它可通过消息来表达。信源可根据消息出现的形式分为两大类型：离散信源和连续信源。在通信系统中，收信者在未收到消息以前，对信源发出什么消息是不确定的，所以可用随机变量或随机变量序列来描述信源输出的消息。信源的数学模型是一个在信源符号集中取值的随机变量序列或随机过程。1

熵最初，熵是一个热力学概念，1865年，由物理学家克劳修斯(R.Clausius，德，1822—1888)提出来。

从统计力学的观点看来，熵表示系统状态自发实现之可能性的程度，所以可以看作为系统不肯定性的度量。因此，在信息论中利用熵的这一概率特征来度量信息。

在信息论中，信息源所包含的平均信息量，称为熵。

随机试验的主要特征，是具有不肯定性，即在试验前，无法肯定会出现哪一种结果。但不同随机试验的不肯定程度是有差别的。“熵”就在数值上描述出各种随机试验本身不肯定的程度，利用它，就有可能进行比较。

设试验a有k个结果：A1、A2、…Ak，考虑到各个结果出现可能性的不同，关于a不肯定性的度量

H(a)=c[P(A1)log P(A1)+P(A2)logP(A2+…+P(Ak)log P(Ak)]，称为试验a的熵。其中c为常数，与选用的单位有关;P(Ai)为Ai的概率。

上述结果与统计热力学某些公式的类似性，导致香农(C.E.Shannon，美，1916—2001)使用热力学术语“熵”来命名平均信息量。

在热力学、统计力学、信息论、概率论中，熵有重要意义;至今，在控制论、经济学、生物学等学科的研究中，也使用了这一概念。

随机变量亦称随机变数。概率论的基本概念之一，是取值具有随机性，能表示随机现象各种结果的变量。许多随机试验的结果本身就是数量，如射击命中的环数，掷骰子掷出的点数等。有些随机试验的结果虽然只是定性的，非数量的，但人们可以做出对应，使其结果用数字表示.例如，掷一枚硬币，可以用1表示“出现正面”，用0表示“出现反面”.一般地，定义在基本事件空间Ω上的单值实函数ξ(ω)就称为随机变量。自然，为了能对这种函数作概率描述，还应当对它们作某些限制。

随机变量的严格定义如下：(Ω，F，P)为概率空间，ξ=ξ(ω) (ω∈Ω)是定义在Ω上的单值实函数，若对于任一实数x，ω的集合{ω∶ξ(ω)≤x}是一随机事件，亦即{ω|ξ(ω)≤x}∈F，则称ξ(ω)为随机变量。条件{ω|ξ(ω)≤x}∈F也可改为对于直线上的任一波莱尔点集B∈B1，有{ω|ξ(ω)∈B}∈F。

实质上，随机变量就是概率空间(Ω，F，P)上的F可测函数.随机变量的引进和研究是概率论发展中的重大事件.由于随机变量是取数值的，因此可以对它进行各种数学运算，这给概率论的研究带来了极大的方便。1

本词条内容贡献者为:

王海侠 - 副教授 - 南京理工大学