[科普中国]-霍普夫纤维化

霍普夫纤维化（Hopf fibration）是一个基本概念，是来自复射影空间的构造。

简介霍普夫纤维化是一个基本概念，是来自复射影空间的构造。

设π:Cm+1\{0}→CPm是自然投影，若把Cm+1看做实矢量空间R2(m+1)，则方程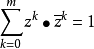在R2(m+1)中定义了一个2m+1维的单位球面S2m+1上。若将π限制在S2m+1上，则得π:S2m+1→CPm。对于任意p∈CPm，逆像π-1(p)是一个圆周，这称为S2m+1的霍普夫纤维化。1

复射影空间复射影空间是实射影空间的推广，即复欧氏空间添加无穷远点构成的空间。

添加了无穷远点的复平面称为一维复射影空间，记为CP1，推广到n维，便得到n维复射影空间。

实向量空间实数体R上的向量空间叫实向量空间。

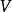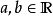一个实向量空间是具有两个合成法则的集合（所有及所有）：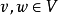

(a)向量加法:；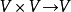

(b)标量乘法：；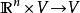

本词条内容贡献者为:

杜强 - 高级工程师 - 中国科学院工程热物理研究所