[科普中国]-第二类椭圆函数

概念基础——椭圆函数简介

椭圆函数也叫第一类椭圆函数，是第二、第三类椭圆函数的基本，双周期亚纯函数的统称。在历史上，椭圆函数是作为椭圆积分的反函数而引入的，故名。

设2ω，2ω'为椭圆函数 f(z) 的两个基本周期，且

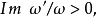
f(z) 在以任意一点 z 及 z+2ω，z+2ω+2ω'，z+2ω' 为顶点的平行四边形（称为周期平行四边形）内极点的个数（n阶极点算作n个极点）称为椭圆函数 f(z) 的阶。1

椭圆函数的性质椭圆函数具有下列性质：

1、若 f(z) 为椭圆函数，则其任意阶导数 f(n)(z) 也是椭圆函数，基本周期不变；

2、椭圆函数的阶有限；

3、刘维尔第一定理：零阶椭圆函数必为常数；

4、刘维尔第二定理：椭圆函数在任一周期平行四边形内各极点处留数之和必为0；

因此，椭圆函数在任一周期平行四边形内不可能只有一个（一阶）极点。换言之，不存在一阶椭圆函数。

5、椭圆函数在任一周期平行四边形内零点的个数（n阶零点算作n个零点）等于它的阶；

6、刘维尔第三定理：对于任一常数C，方程 f(z)=C 在周期平行四边形内根的个数（n重根算作n个根）等于 f(z) 的阶；

7、刘维尔第四定理：在一个周期平行四边形内，椭圆函数零点ak(k=1,2,…)之和与极点bk(k=1,2,…)之和相差某一周期，即

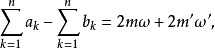m，m'为整数。

最简单的椭圆函数是二阶椭圆函数。在这些函数中，或者把（在任一周期平行四边形中）具有一个二阶极点（留数为0）的函数选作标准函数（外尔斯特拉斯椭圆函数），或者把具有两个一阶极点（留数互相抵消）的函数选作标准函数（雅克比椭圆函数）。1

第二类椭圆函数第二类椭圆函数是椭圆函数的推广之一。如果亚纯函数 f(u) 满足

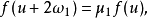
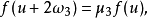（ω1，ω3及μ1，μ3均为常数），则称 f(u) 为第二类椭圆函数。

例如，

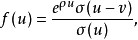其中 σ(u) 为外尔斯特拉斯 σ 函数，ρ 及 v 为常数。此时。

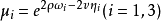2ω1及2ω3 仍称为第二类椭圆函数的基本周期。1