[科普中国]-开尔文函数

开尔文函数1(Kelvin function)有两大类函数，两大类分别由实部和虚部构成。实部分别对应ber(x)、ker(x)，虚部分别对应为bei(x)、kei(x)。

简介开尔文函数有两类。第一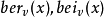类；第二类

第一类开尔文函数ber（x）对于整数n，bern（x）有系列扩展

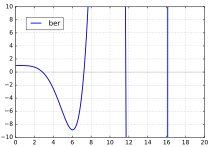
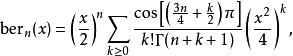其中Γ（z）是伽马函数。特殊情况ber0（x），通常表示为ber（x），具有系列扩张

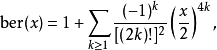和渐近系列

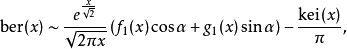其中

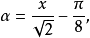
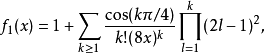
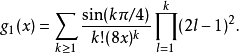
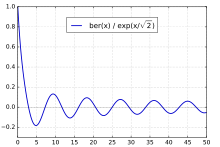
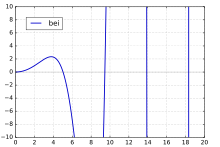
bei（x）对于整数n，bein（x）具有系列扩展

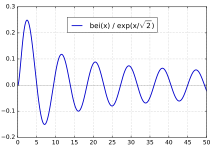
特殊情况bei0（x），通常表示为bei（x），具有序列扩张

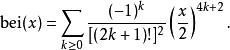和渐近系列

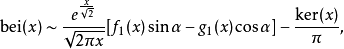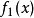其中α， ，和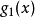 被定义为ber（x）2。

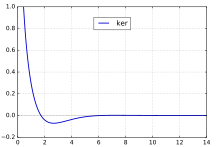
第二类开尔文函数ker（x）特殊情况ker0（x），通常表示为ker（x），具有序列扩展

和渐近级数

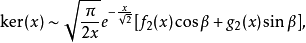其中

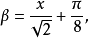
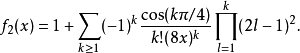
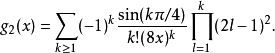
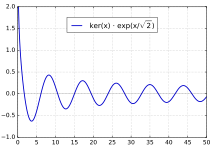
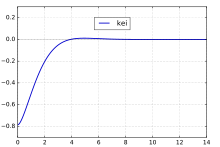
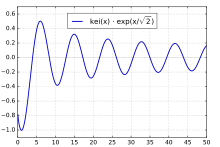
kei（x）通常表示为kei（x）的特例kei0（x）具有系列扩张

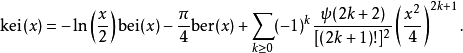和渐近级数

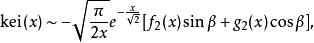其中β，f2（x）和g2（x）被定义为ker（x）3。

本词条内容贡献者为:

王海侠 - 副教授 - 南京理工大学