[科普中国]-算术关系

算术关系(arithmetical relation)是递归关系的推广，是可以通过对递归关系添加有穷个量词定义的关系，即可以表示Q1x1Q2x2…QnxnR(x1，x2，…，xn，a1，a2，…，an)形的关系，其中R为递归关系，Q1，Q2，…，Qn为一阶量词∃或ᗄ1。

基本介绍算术关系是可以通过对递归关系添加有穷个量词定义的关系，即可以表示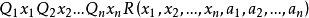形的关系，其中R为递归关系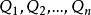，为一阶量词∃或ᗄ。等价地，算术关系亦是可以从递归关系出发，经有限次否定与射影运算得到的关系。算术关系的定义是由美国逻辑学家、数学家克林(S.C.Kleene)与波兰数学家莫斯托夫斯基(A.Mostowski)给出的。从可判定(或可计算)的角度上说，递归关系具有最小的复杂性，但递归关系对(不受限)量词不封闭，而算术关系类则为递归关系类对量词封闭的最小扩张，因此算术关系的概念可看做递归关系概念的推广，实际上，任何算术关系也恰为一阶算术可定义关系(参见“算术表示定理”)，这也是“算术”一词的来源1。

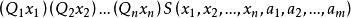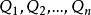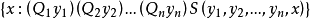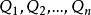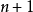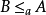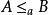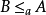相关性质与概念相对算术关系相对算术关系(relativized arithmetical relation)是算术关系概念的相对化。对自然数集A和关系R，若R可表示成的形式，其中为量词ᗄ或∃，S为相对A递归的关系，则称R为相对于A的算术关系。若集合B是相对于A的(一元)算术关系，即B可表示成：其中为量词，S为相对于A递归的元关系，则称B为相对于A的算术集，并记为，亦称B可算术化归到A。由算术化归关系可导出算术等价的概念。对集合A，B，若，并且，则称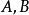算术等价，记为。

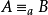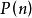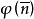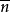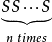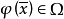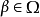算术性算术性(arithmeticity)是递归论术语，反映数论谓词(关系)能否由一阶算术理论来表示的性质，数论谓词P具有算术性(即称P为算术谓词、或算术关系)，是指存在一个一阶算术公式φ在Ω中表示P，即对任何自然数n，成立，当且仅当(为0)是Ω中的真语句，所有丢番图关系都是算术关系，从而由马蒂雅塞维奇(A.Matijasevich)-鲁宾孙(J.B.Robinson)-戴维斯(M.D.Davis)-普特南(H.Putnam)关于希尔伯特第10问题的解答知，所有递归关系都是算术关系。实际上，所有算术关系都是由递归关系出发经过逻辑运算而得到的，关于算术性的最引人注目的结论是波兰学者塔尔斯基(Tarski，A.)于1933年证明的定理：算术的真假性不是算术的，即不存在一个算术公式φ，使，当且仅当(在某种确定的编码之下)以为编码的算术公式β是算术地真的(即)1。

算术表示定理算术表示定理(arithmetical representation theorem)指算术关系可用一阶算术公式表示的定理。它指出：一关系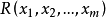为算术关系(即R在算术分层中)，当且仅当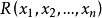在一阶算术中可定义.即存在一阶算术中的公式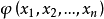，使得对任何自然数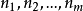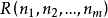，为真，当且仅当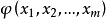在一阶算术中为真，这也是“算术分层”与“算术关系”一词的来源，算术表示定理是美籍奥地利数学家哥德尔()于1931年证明的1。

本词条内容贡献者为:

尚华娟 - 副教授 - 上海财经大学