[科普中国]-第一类贝塞尔函数

历史

贝塞尔函数的几个正整数阶特例早在18世纪中叶就由瑞士数学家丹尼尔·伯努利在研究悬链振动时提出了，当时引起了数学界的兴趣。丹尼尔的叔叔雅各布·伯努利，欧拉、拉格朗日等数学大师对贝塞尔函数的研究作出过重要贡献。1817年，德国数学家贝塞尔在研究开普勒提出的三体引力系统的运动问题时，第一次系统地提出了贝塞尔函数的总体理论框架，后人以他的名字来命名了这种函数。2

现实背景和应用范围贝塞尔方程是在圆柱坐标或球坐标下使用分离变量法求解拉普拉斯方程和亥姆霍兹方程时得到的（在圆柱域问题中得到的是整阶形式 α =n；在球形域问题中得到的是半奇数阶形式 α =n+½），因此贝塞尔函数在波动问题以及各种涉及有势场的问题中占有非常重要的地位，最典型的问题有：

（1）在圆柱形波导中的电磁波传播问题；

（2）圆柱体中的热传导问题；

（3）圆形（或环形）薄膜的振动模态分析问题；

在其他一些领域，贝塞尔函数也相当有用。譬如在信号处理中的调频合成（FM synthesis）或凯泽窗（Kaiser window）的定义中，都要用到贝塞尔函数。3

第一类贝塞尔函数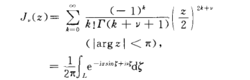贝塞尔方程是一个二阶常微分方程

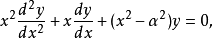必然存在两个线性无关的解。针对各种具体情况，人们提出了表示这些解的不同形式。

第一类贝塞尔函数(Bessel function of the first kind)作为贝塞尔方程的第一解，又称贝塞尔函数，有时会简称为 J 函数，记作Jα。

第一类α阶贝塞尔函数Jα(x)是贝塞尔方程当α为整数或α非负时的解，须满足在x= 0 时有限。另一种定义方法是通过它在x= 0 点的泰勒级数展开（或者更一般地通过幂级数展开，这适用于α为非整数）：

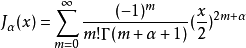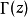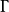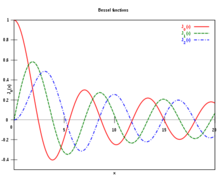
上式中 为 函数（它可视为阶乘函数向非整型自变量的推广）。第一类贝塞尔函数的形状大致与按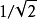 速率衰减的正弦或余弦函数类似，但它们的零点并不是周期性的，另外随着''x''的增加，零点的间隔会越来越接近周期性。右图所示为0阶、1阶和2阶第一类贝塞尔函数。

如果α不为整数，则Jα(x)和J−α(x)线性无关，可以构成微分方程的一个解系。反之若α是整数，那么上面两个函数之间满足如下关系：

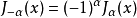于是两函数之间已不满足线性无关条件。为寻找在此情况下微分方程与Jα(x)线性无关的另一解，需要定义第二类贝塞尔函数。3

贝塞尔积分α为整数时贝塞尔函数的另一种定义方法由下面的积分给出：

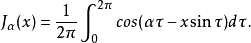这个积分式就是贝塞尔当年提出的定义，而且他还从该定义中推出了函数的一些性质。另一种积分表达式为3：

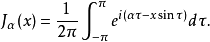
和超几何级数的关系贝塞尔函数可以用超几何级数表示成下面的形式：

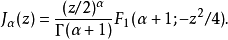
ɑ为整数，由于函数线性相依的特性(用了一个，少了一个，所以要再弄出一个出来)，才需定义Neumann函数（即第二类贝塞尔函数）。3