[科普中国]-回归诊断

概念

回归诊断主要用于检验关于回归假设是否成立，以及检验模型形式是否错误，否则我们通过最小二乘法求得的回归方程就缺乏理论依据。这些检验主要探究的问题为：

1） 残差是否为随机性、是否为正态性、是否不为异方差；

2）高度相关的自变量是否引起了共线性；

3）模型的函数形式是否错误或在模型中是否缺少重要的自变量；

4）样本数据中是否存在异常值。

发展历程随着高速电子计算机的日益广泛应用，回归分析愈来愈成为各个领域科技工作者分析数据的一种常用工具。但是，在长期地广泛实际应用中，人们逐渐地发现经典的最小二乘估计的结果并不总是令人满意，于是统计学家们从多方面进行努力试图改进最小二乘估计，例如，为了克服设计阵的病态性，提出了以岭估计为代表的多种有偏估计。为了解决自变量个数较多的大型回归模型的变量取舍问题，提出了众多的回归自变量选择准则和算法。为了克服最小二乘估计对异常值的敏感性，提出了各种稳健回归。为了考察模型假设条件的合理性及数据对统计推断影响大小，逐渐发展起来了“回归诊断”这一新的研究领域。以上诸方面的新结果构成了回归分析近期发展的主体。

分类从总体上讲，回归诊断尚属较新的研究分支，因此关于它的研究范围及采用的术语，在各家笔下也不尽相同。这里，把残差分析、数据变换和影响分析等统统包罗在回归诊断这个总题目下。这是因为残差分析和数据变换可以看作模型的诊断，而影响分析则看作数据的诊断1。

1.残差分析回归诊断中要解决的第一个基本问题——模型假设的合理性，不少文献概括为残差分析。这是因为这个问题的解决在很大程度是靠对残差作种种统计分析来实现。

在回归诊断中，残差分析的发展虽然相对说来比较早,但也只是廿年前的事.究其原因主要是这类问题计算量都很大,只有现代电子计算技术得到广泛应用之后,它的研究和应用才能成为可能。

残差是最重要的一种回归诊断量,它蕴含了有关模型基本假设的许多重要信息。残差分折就是对残差进行统计处理，从中提炼出这些信息的方法.基于不同的考虑和模型的不同用处，人们定义了许多种残差——普通残差，学生化残差，递归残差、偏残差等。

残差图是残差分析的一个重要工具.它通过简单的图示直观地显示出残差的各种趋势，以更方便诊断出模型假设的某些不合理性。

2.数据变换当对数据作了残差分析，,发现模型的某些假设不满足或不能近似满足时，我们需要对数据作适当变换。在这里，最重要的变换类是Box-Cox的幂变换，它已得到广泛应用。

这方面的近期研究多集中在如下三方面：

1.针对特殊分布类的Box-Cox变换的修正；

2.变换参数的估计；

3.数据对变换参数的影响。

3.影响分析回归诊断所要研究的另一个重要问题是，探查对统计推断(如估计或预测)有较大影响的试验数据。说话方便起见,我们沿用一些文献的术语,称其为影响分析（Influence Analysis）。

与残差分析相比,影响分析的发展比较晚，大致是十年前的事。但近年来发展比较快,虽然目前的研究还局限于一组数据或多组数据的影响问题,但研究的领域已经远远超出了线性回归的范围，在非线性回归,1091就回归，时间序列分析以及主成分分析等方面已经出现了一些工作。

一般说来，我们期望每组数据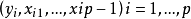 对统计推断都有一定影响，但这种影响又不要过大，不然的话，如果某组数据的影响过大,那末包含这组数据的经验回归方程与不包含这组数据的经验回归方程差异很大，于是经验回归方程关于数据就不具有“稳定”性。

在这里，需要研究两个基本问题：一是模型扰动的方式；二是度量扰动对统计推断影响大小的标准。

对前一问题，目前的研究所采用的扰动方式多为每次剔除一组或多组数据.这似乎没有更多讨论的余地.而对后一个问题，人们从各种不同的角度出发，提出了许多度量影响的标准。如Cook距离、AP-统计量、似然距离等2。

未来发展目前，回归诊断已经有了一定的发展，但现有的结果还远远不能满足应用实践的需要。为了不同的目的,还需要引进一些新的诊断量。此外，诊断方法一般计算量都很大，因此建立节省的算法也是很迫切的。面对着这些情况,对回归诊断的研究提出了一些原则3，归纳起来主要有

1.诊断方法在正确模型和某些条件不满足的模型下的统计性质应该是已知的或近似已知；

2.诊断量应当尽可能从模型参数化来导出,这样就把模型诊断问题归结为参数推断；

3.好的诊断量应当有有效的图法；

4.诊断方法本身应该建议数据的“治疗”方案。