[科普中国]-超球微分方程

超球微分方程(hyperspherical equation)是数学物理中常见的常微分方程之一。连带勒让德方程经因变量变换后，可以得到超球微分方程；勒让德方程和格根鲍尔方程都是它的特殊情形。

概念超球微分方程(hyperspherical equation)是数学物理中常见的常微分方程之一。形式为：

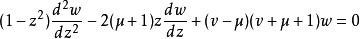连带勒让德方程经因变量变换后，可以得到超球微分方程；勒让德方程和格根鲍尔方程都是它的特殊情形。1

数学物理以研究物理问题为目标的数学理论和数学方法。它探讨物理现象的数学模型，即寻求物理现象的数学描述，并对模型已确立的物理问题研究其数学解法，然后根据解答来诠释和预见物理现象，或者根据物理事实来修正原有的模型。

最早的物理问题研究就与数学息息相关。公元前6世纪古希腊毕达哥拉斯学派用整数之比论述琴弦的振动，发展起一套音乐理论。公元前3世纪阿基米德使用严格的几何方法论证力学原理，求出若干平面图形的重心。他还应用浮力定律研究旋转抛物体在流体中的稳定性，应用杠杆原理得到许多几何图形的面积。公元2世纪托勒密利用三角方法研究光学。这些都是数学物理的早期例子。2

文艺复兴以后，数学物理有了长足发展。17世纪初意大利科学家伽利略建立了落体运动的正确定律;德国科学家开普勒发现行星运动三大定律;1666年牛顿建立起万有引力定律，1686—1687年完成巨著《自然哲学的数学原理》，以牛顿运动三定律为基础建立起牛顿力学体系。其中的三体问题和各种经典的动力系统都是数学物理长期研究的对象。

微积分的发明为解决各种物理和力学问题提供了有力工具。对三体问题、摆的运动及弹性理论等问题的数学刻画引导出一系列常微分方程，求解这些方程就成为牛顿力学中的重要数学问题。到18世纪，对弦振动问题、电磁场理论、流体力学和热传导等问题的深入研究开始了偏微分方程和偏微分方程组的研究，后人将这些偏微分方程以及具有物理意义的积分方程、微分积分方程和常微分方程统称为数学物理方程。从17世纪末开始，对最速降线问题、等周问题的讨论引发了变分法的创立。到18世纪中期，牛顿力学的基础开始由变分原理刻画，此后许多物理理论都以变分原理作为自己的基础。

19世纪末由动力系统内行星和卫星轨道的稳定性问题导致微分方程定性理论的发展，到20世纪初，数学物理方程成为数学物理的主要内容。此后，等离子物理、固体物理、非线性光学、空间技术、核技术等方面不断提出新的偏微分方程问题，使数学物理方程的内容进一步丰富起来，同时对这些方程的研究也促进了复变函数论、积分变换、特殊函数、变分法、调和分析、泛函分析乃至微分几何学、代数几何学、拓扑学等数学分支的发展。

20世纪初，对电磁理论和引力场的研究，使闵科夫斯基空间和黎曼空间的几何大大发展，成为爱因斯坦狭义相对论和广义相对论的基础。许多物理量以向量、张量和旋量作为表达式。20世纪20年代量子力学的诞生依赖于希尔伯特空间理论，并应用了算子的谱理论，量子力学发展成为量子场论时，再次应用了泛函分析的新工具，即20世纪30年代由匈牙利—美国数学家冯·诺伊曼发展起来的算子代数理论。20世纪40—50年代核结构和基本粒子理论兴起时，另一位匈牙利一美国数学家威格纳开创的群表示论又成为主要工具。这些理论在数学的其他分支也起着重要作用。

近几十年来，对基本粒子的内在对称性研究导致了杨振宁—米尔斯理论(即规范场理论)的产生，并推动了纤维丛理论的发展；对经典统计物理学的研究促进了统计理论的深入研究；应用电子计算机后又发展起计算力学、计算物理等学科。数学物理内容日益丰富，同时又促进了数学的发展，成为产生数学新思想、新问题及新方法的一个源泉。数学物理中的许多方法和结果对数学在其他学科中的应用起了借鉴作用，推动了诸学科的发展。

常微分方程分析数学的重要分支之一。包括一个自变量和它的未知函数以及未知函数的微商的等式叫做常微分方程。常微分方程研究的内容包括解的基本性质(如存在性、唯一性等)，解的解析表达式或近似的解析表达式，解的定性性质(如运动稳定性、周期解的存在性等)以及解的数值解法。

常微分方程的发展历史大体可分为四个阶段：18世纪及其以前;19世纪初期和中期；19世纪末期及20世纪初期；20世纪中期以后。

19世纪末和20世纪初是常微分方程发展的第三个阶段，主要在以下三个方面有重大发展：首先是关于常微分方程的解析理论的研究(见常微分方程解析理论)，其次是常微分方程实域定性理论的创立(见常微分方程定性理论)，第三是常微分方程摄动理论即小参数理论的建立。

从20世纪中期起，常微分方程的发展既深又广，进入了一个新的阶段，有以下几方面的工作。

由于工程技术的需要而产生了新型问题和新的分支。例如工程控制论中火箭发动机的燃烧过程由于时滞现象而产生的带有时滞的常微分方程(或称微分差分方程)，以及更广义的泛函微分方程。又如由于空气中的湍流对飞机运动的影响，使微分方程中带有随机摄动项，这类问题产生了随机微分方程。

由于应用问题的需要而产生了一些近似的解析形式的解的求法。

电子计算机的出现与发展推动了常微分方程的研究，并取得一系列成果。起初，常微分方程由于解析解难求而转向定性研究，当定性研究也困难时，又转而用计算机“强攻”，得出一定的数值模拟结果后，反过来为定性研究提供了感性的新信息。这方面的研究正在兴起。

常微分方程理论本身向高维数、抽象化的方向发展。例如从普通空间常微分方程向抽象空间常微分方程发展，从具体动力系统向抽象动力系统的发展，从实域定性理论向复域定性理论的发展等等。1

连带勒让德方程数学物理中常见的常微分方程之一。其形式为：

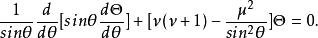作变换：

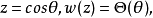又可写成：

此方程有三个奇点(±1，∞)，且均为正则奇点，故可化为超几何方程。

在球坐标系下将拉普拉斯方程或亥姆霍兹方程分离变量时，可出现连带勒让德方程。

本词条内容贡献者为:

尚华娟 - 副教授 - 上海财经大学