[科普中国]-双轴球面函数

双轴球面函数(biaxial spherical surface function)是在坐标系中改变极轴方向时出现的球函数。

概念双轴球面函数(biaxial spherical surface function)是在坐标系中改变极轴方向时出现的球函数。设空间两点的直角坐标为(x，y，z)和(x′，y′，z′)，相应的球坐标为(r，θ，φ，)和(r′，θ′，φ′).(θ，φ)方向与(θ′，φ′)方向的夹角为γ(如图)，

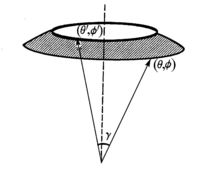
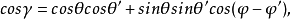则：

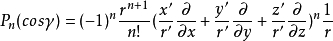为双轴球面函数，即以(θ′，φ′)方向为极轴时(θ，φ)方向的球面函数。它可以用两各别方向的球面函数表示：

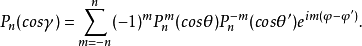这个公式又称为勒让德多项式的加法定理。1

球函数通常指连带勒让德方程的解，亦即连带勒让德函数。有时也把面调和函数称为球函数。在球坐标系中用分离变量法解拉普拉斯方程或亥姆霍兹方程时可出现这些函数。

在现代数学中，球函数及其推广已被广泛应用于拓扑群的酉表示。2

连带勒让德方程连带勒让德方程（Associated Legender equation) 是一个二阶常微分方程。

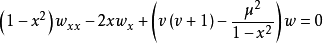如果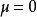 ，连带勒让德方程化为勒让德方程：

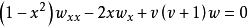
连带勒让德方程的解为：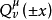

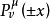
微分方程微分方程指含有未知函数及其导数的关系式。解微分方程就是找出未知函数。

微分方程是伴随着微积分学一起发展起来的。微积分学的奠基人Newton和Leibniz的著作中都处理过与微分方程有关的问题。微分方程的应用十分广泛，可以解决许多与导数有关的问题。物理中许多涉及变力的运动学、动力学问题，如空气的阻力为速度函数的落体运动等问题，很多可以用微分方程求解。此外，微分方程在化学、工程学、经济学和人口统计等领域都有应用。

数学领域对微分方程的研究着重在几个不同的面向，但大多数都是关心微分方程的解。只有少数简单的微分方程可以求得解析解。不过即使没有找到其解析解，仍然可以确认其解的部分性质。在无法求得解析解时，可以利用数值分析的方式，利用电脑来找到其数值解。动力系统理论强调对于微分方程系统的量化分析，而许多数值方法可以计算微分方程的数值解，且有一定的准确度。

含有未知函数的导数，如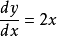的方程是微分方程。 一般的凡是表示未知函数、未知函数的导数与自变量之间的关系的方程，叫做微分方程。未知函数是一元函数的，叫常微分方程；未知函数是多元函数的叫做偏微分方程。微分方程有时也简称方程1。

球坐标系球坐标系是三维坐标系的一种，用以确定三维空间中点、线、面以及体的位置，它以坐标原点为参考点，由方位角、仰角和距离构成。球坐标系在地理学、天文学中都有着广泛应用。

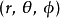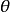在学术界内，关于球坐标系的标记有好几个不同的约定。按照国际标准化组织建立的约定（ISO 31-11），径向距离、天顶角、方位角，分别标记为。这种标记在世界各地有许多使用者。通常，物理界的学者也采用这种标记。而在数学界，天顶角与方位角的标记正好相反：被用来代表天顶角，被用来代表方位角。数学界的球坐标标记是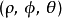。这种标记的优点是较广的相容性；在二维极坐标系与三维圆柱坐标系里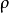，都同样地代表径向距离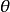，也都同样地代表方位角。本条目采用的是物理标记约定。

在数学里，球坐标系（英语：Spherical coordinate system）是一种利用球坐标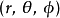表示一个点 p 在三维空间的位置的三维正交坐标系。右图显示了球坐标的几何意义：原点与点 P 之间的径向距离 r ，原点到点 P 的连线与正 z-轴之间的天顶角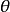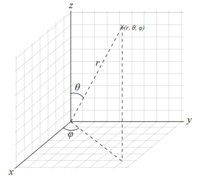以及原点到点 P 的连线，在 xy-平面的投影线，与正 x-轴之间的方位角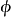。3

本词条内容贡献者为:

尚华娟 - 副教授 - 上海财经大学