[科普中国]-超几何级数

定义

超几何级数亦称高斯级数，是超几何方程在单位圆内的第一解。

求和项是超几何项的级数称为超几何级数，常用如下记号表示

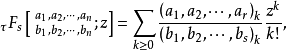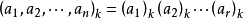其中且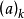表示升阶乘，即。

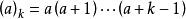超几何项【bypergeometric term】

超几何项

定义在自然数上的函数f(n)被称为超几何项，如果f(n+1)/f(n)是关于n的有理函数，即存在多项式p(n)和q(n)使得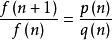可以表示为有限个超几何项的线性组合的函数被称为闭形式（closed form）。

双超几何项如果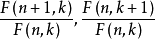都是关于n和k的有理函数，F(n，k)称为双超几何项（hypergeometric term in both arguments）。

正则超几何项组合恒等式机器证明的主要研究对象是一类特殊的双超几何项，被称为正则超几何项（proper bypergeometric term ），它是如下形式的二元函数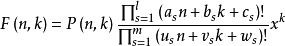，其中x是不定元，且：

（1）P(n，k)是关于n，k的多项式；

（2）a𝘴，b𝘴，u𝘴，v𝘴都是整数；

（3）c𝘴，w𝘴是可以含其他未定参数的常数；

（4）l和m是非负整数。

若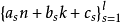中没有负整数，则具有如上形式的F在点(n，k)是有定义的。若F在(n，k)点有定义，且P(n，k)=0，或至少有一个是负整数，则认为F(n，k)=0。

例如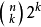，是正则超几何项，因为它可以写成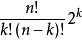满足定义。又如，虽然F(n,k)=1/(n+3k+1)看起来不是正则超几何项的形式，但是它可以写成如下形式:

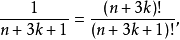
所以它也是正则超几何项。可以证明F(n,k)=1/(n²+k²+1)不是正则超几何项。1