[科普中国]-复合泊松分布

在概率论中，复合泊松分布是指一些独立同分布的随机变量的和的概率分布，而这些随机变量的个数服从泊松分布。在最简单的情形下，复合泊松分布可以是连续分布或者离散分布。

简介在概率论中，复合泊松分布是指一些独立同分布的随机变量的和的概率分布，而这些随机变量的个数服从泊松分布。在最简单的情形下，复合泊松分布可以是连续分布或者离散分布。

定义假设

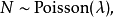也就是说，N是一个随机变量，其分布为期望为λ的泊松分布，且

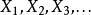
为同分布的随机变量，他们相互独立，且与N也独立。则在变量个数（N）给定的条件下，这N个独立同分布的随机变量和的概率分布：

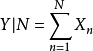是一个良定的分布。N= 0时，Y也为0，此时Y|N=0有退化的分布。

复合泊松分布可以通过将(Y,N)的联合分布在N上边缘化而得到，而联合分布可以通过结合条件分布Y|N和N的边缘分布而得到。1

复合泊松过程一个速率为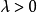 ，增量分布为G的复合泊松过程是一个连续时间随机过程 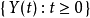，定义如下

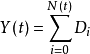其中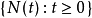， 是一个速率为 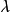的泊松过程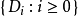， 是独立同分布的随机变量，其分布为G，与 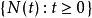独立。1

应用复合泊松分布广泛用于精算学和保险业，用来对总索赔额Y进行建模，Y是随机的N个独立同分布的索赔额X1,X2, ... ,XN的和。1

参见概率论

机率分布

本词条内容贡献者为:

杜强 - 高级工程师 - 中国科学院工程热物理研究所