[科普中国]-多维随机样本均值向量

多维随机样本均值向量亦称样本均值，多元分析的基本概念之一，是对多维随机样本取平均值所得的向量。

简介多维随机样本均值向量亦称样本均值，多元分析的基本概念之一，是对多维随机样本取平均值所得的向量。

具体作法是对每个分量的抽样取平均值。这里的样本是

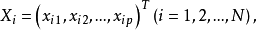
每个分量的平均值是

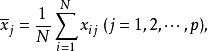
则称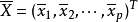为 p 维随机样本的平均值向量，即 p 维随机样本均值向量。1

多元分析统计学的一个重要分支，主要探究多维数据的内在规律性，如多维随机变量间的相互依赖关系、结构关系等。根据获得数据的类型不同，多元统计分析可分为连续型和离散型多元分析，前者包括多元正态分布的估计与检验、多因变量线性回归、判别分析、典型相关分析、主成分分析、因子分析、聚类分析等，后者包括列联表分析、对数线性模型、对数单位模型、逻辑斯谛回归模型、有序离散型多元变量的分析。包括3类：

①多元方差分析、多元回归分析和协方差分析，称为线性模型方法，用以研究确定的自变量与因变量之间的关系；

②判别函数分析和聚类分析,用以研究对事物的分类；

③主成分分析、典型相关和因素分析，研究如何用较少的综合因素代替为数较多的原始变量。

本词条内容贡献者为:

王海侠 - 副教授 - 南京理工大学