[科普中国]-常微分方程数值解法

简介

作为数值分析的基础内容，常微分方程数值解法的研究已发展得相当成熟，理论上也颇为完善，各类有实用价值的算法已经建立，并已形成计算机软件。它处理问题的思路与方法常可用于偏微分方程的数值求解。主要研究以下三类定解问题的数值解法：初值问题、两点边值问题与特征值问题。初值问题的数值解法应用广泛，是常微分方程数值解法的主要内容。在这方面有突出贡献的学者当推达赫奎斯特（Dahlquist，G.）、巴特赫尔（Butcher，J.C.）及吉尔（Gear，C.W.）等人。两点边值问题及特征值问题的研究相对较为薄弱，其中凯勒尔（Keller，H.B.）的工作影响较大。1

基本途径构造常微分方程数值算法的基本途径有：

1、用差商替代导数。将微分问题中未知函数及其导数分别用在某些离散点处函数值的组合与差商近似替代。

2、数值积分法。将微分问题转化为等价的积分方程问题，用各种数值积分公式近似计算未知函数的积分。

3、待定系数法。把欲构造的计算公式写成在离散点函数值之线性组合的待定系数形式，利用函数的泰勒展开式与对公式的精度要求，确定公式的系数。

4、加权余量法。根据微分方程余量极小化的要求，确定计算公式。1

基本问题常微分方程数值解法研究的基本问题有：

1、构造计算公式；

2、研究算法的相容性、精度阶与收敛性，估计局部与整体截断误差；

3、研究在计算过程中舍入误差传播与积累的规律，即方法的稳定性问题；

4、算法的数值实现问题，力图以较小的计算工作量与可靠的软件系统，在计算机上给出满足精度要求的计算结果。1

常微分方程初值问题数值解法指研究求解初值问题各类数值方法的构造、理论分析与数值实现问题。研究的主要对象为一阶方程组初值问题

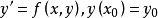式中 y 及 f 均为向量函数。对于高阶方程的问题，约定已事先用引进新未知数的办法化为一阶方程组。在研究中，需要把问题区分为两大类：非刚性问题与刚性问题。这是根据问题之解的数学性质来区分的。传统的数值方法（例如，经典龙格库塔法等）适用于非刚性问题，而对刚性问题则需要构造新的计算公式，这是因为，此类问题对数值方法的稳定性有特殊要求。1