[科普中国]-拓扑熵

拓扑熵（topology entropy）是分形几何中的一个重要概念。

分形几何学是一门以不规则几何形态为研究对象的几何学。

简介拓扑熵是分形几何中的一个重要概念。

设X为紧度量空间，T:X→X为连续映射，设α={A1,A2,…,An}为X的一个有限开覆盖，令N(α)表示α的所有子覆盖的最小基数，则T对于α的拓扑熵定义为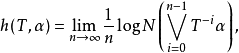T的拓扑熵定义为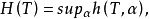其中α取遍X的有限开覆盖。1

开覆盖（open cover）

{X}的开子集的集合{Oα}叫A包含于X的一个开覆盖，若A∪Oα包含于（表示{Oα}所有元素的并集）。

分形几何分形几何学是一门以不规则几何形态为研究对象的几何学。相对于传统几何学的研究对象为整数维数，如，零维的点、一维的线、二维的面、三维的立体乃至四维的时空。

分形几何学的研究对象为非负实数维数，如0.63、1.58、2.72、log2/log3（参见康托尔集）。因为它的研究对象普遍存在于自然界中，因此分形几何学又被称为“大自然的几何学”。

本词条内容贡献者为:

胡启洲 - 副教授 - 南京理工大学