[科普中国]-维塔利覆盖引理

在一个度量空间中有一族闭球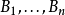，则这一族球中存在互不相交的球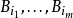，适合条件

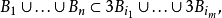
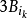表示和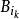有相同中心，而半径是的三倍的球。

在一个度量空间中有一族半径为正数的闭球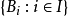，这族球的半径有有限的上界，即

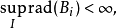则这一族球中存在互不相交的球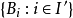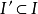，，适合条件

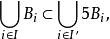
表示和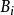有相同中心，而半径是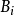的五倍的球。1

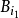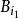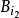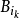取这一族球中半径最大的一个球，然后除去所有与相交的球。再从剩下的球中取半径最大的为，如此类推。那么任何其他的球必定因为和某个相交而被除去，这个球的半径不大于，因此包含在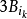之内。

设这一族球的半径的上确界为R。将这一族按半径分成子集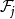，j为正整数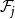；包含半径在区间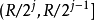的球。依次取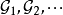如下：

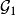设。取为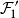内互不相交球的子集之中的极大者，即其他在中的球都与这一子集中某个球相交。从佐恩引理知这样的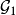存在，以下同。

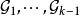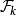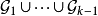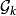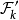设已取，k为某大于1的整数。设是中不与中任何球相交的全部球的子集。取为内互不相交球的子集之中的极大者。

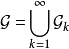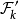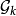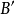设。任何其他的球B必在某一个中，因此这个球与中一个球相交，而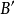的半径大于B的半径的二分之一，故此B包含在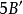之内。2

因为有无限多球时，可能不存在半径最大的球，所以在构造中，每一步选择的球的半径，只要求接近余下的球的半径的上确界。而结果中的5并非最佳常数。将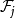的定义中的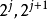的2换成任何大于1的数c，那么就可把结果中的5换成1+2c，即可以用任何大于3的数取代。不过由于未必有半径最大的球，以致不能像有限多球时用3取代，以下是一个简单例子。

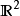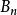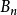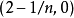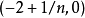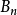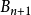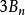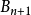在平面中，给出如下的一族球：对每个正整数n，是半径为的闭球，若n为奇数，的圆心在；若n为偶数，则圆心在。所有球都包含原点(0,0)，故任意两个球都相交，因此包含互不相交的球的子集只能有一个球。这一族球的半径上确界是2，然而全部球的半径都小于2。若选任何一个为这个子集，因有半径更大的球在原点的另一侧，故此不覆盖。3

这条引理可用于证明哈代－李特尔伍德极大不等式。

贝西科维奇覆盖定理