[科普中国]-法图集

概念

法图集(Fatou set)是复动力学中的最基本概念。设f(z)为复平面C上的亚纯函数。取U=C，C*=C\{0}，C'分别对应于f为超越整函数、亚纯函数f以z=0为极点和皮卡例外值、其他的亚纯函数。法图集F(f)(或简记为F)定义为：F(f)={z∈U|z是正规点}。茹利亚集J(f)(或简记为J)定义为：J(f)=U\F(f)。1

法图集是开集，茹利亚集是非空完全集。对有理函数R(z)而言，法图集和茹利亚集是完全不变集，即R(J)=J=R'(J)，R(F)=F=R'(F)。对超越亚纯函数f，华歆厚和杨重骏证明了下述不变结果：

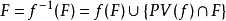
其中，PV(f)为f的皮卡例外值集。

亚纯函数亚纯函数是一类特殊的解析函数。指在z平面上除极点外无其他类型奇点的单值解析函数。如有理函数，tan z等。除极点外为全纯的函数为亚纯函数，它是复变函数论研究的主要对象之一。

德国数学家外尔斯特拉斯、瑞典数学家米塔-列夫勒、法国数学家柯西等都是亚纯函数理论的奠基人。1876年，外尔斯特拉斯证明了一个亚纯函数可以表示为两个整函数的商。第二年，瑞典数学家米塔-列夫勒推广了外尔斯特拉斯的结果，证明在任意一个区域上的亚纯函数皆可表示为两个函数的商，其中每一个都在该区域内解析。法国数学家柯西也曾给出一种分解方法，对相当广的一类亚纯函数得到简单的表示式。

近代亚纯函数理论是20世纪20年代由芬兰数学家奈望林纳所创立。他在1925年发表了亚纯函数的一个一般性理论，这个理论中有两个基本定理分别被称为第一基本定理和第二基本定理，从它们可以推出一系列关于亚纯函数的值分布的结果，丰富并推进了前人的工作，产生了深远影响。

亚纯函数的术语是由法国数学家布里奥和布凯共同引进的。

整函数在平面的有限部分没有奇点的函数，例如多项式e，sinz，cosz等，粗略地说，它们相当于初等实函数的类似物。

整函数是十分重要的一种单值复函数，许多数学家对它进行了深入研究。在这方面的第一个重要结果属于法国数学家柯西，他在1844年证明了每一个有界的整函数是一个常数。后来人们常把这个定理归于刘维尔，因为他在1847年也发表了这个定理。外尔斯特拉斯把实多项式分解为线性因式的定理推广到整函数，大约在1840年，他就得到了整函数的因式分解定理(1876年发表)。1879年，法国数学家皮卡建立了整函数取值范围的重要定理。稍后，法国数学家拉盖尔引进了整函数的格的概念，在某种意义上，它类似于多项式的次数。1883年，庞加莱建立了整函数的模与其格的关系的定理。阿达马研究了与此相反的问题，他在1896年给出了由函数f(z)的最大模的某种界来作出函数零点数的某种上界的估计。1897年，E.波莱尔引入函数增长级的概念，这是度量函数最大模增长速度的特征量，在整函数理论中起着重要作用。2

19世纪末，E.波莱尔综合和改进了皮卡、庞加莱和阿达马的工作，开始形成整函数值分布论。

开集如果点集A中每个点都有一个邻域(例如开区间)，而这个邻域的所有点都是A的点，就称集为A的开集，即一个闭集的余集。开区间(-2，2)就是一个开集，因为-2与2之间的任何点，都位于某一个开区间中;而这些开区间的点都属于(-2，2)。

开集是拓扑空间的基本概念之一。在集合X上确定适当的拓扑结构T后，T中的元素就称为T开集，在不致混淆时亦简称开集。拓扑T亦称为开集系。开集的补集是闭集，开集G的每一点都是G的内点，G也是G的任一点的邻域。开集、闭集、内部、闭包等概念都是康托尔(Cantor，G.(F.P.))在研究欧几里得空间的子集类时引进的。豪斯多夫(Hausdorff，F.)于1914年将它们推广到抽象空间。

皮卡例外值皮卡例外值是整函数理论的一个概念。使f(z)-a仅有有限多个零点的值a称为皮卡例外值。根据皮卡定理，对任一超越整函数至多有一个有穷的皮卡例外值，对超越亚纯函数至多有两个皮卡例外值，例如，e以0为有穷皮卡例外值，sin z无有穷皮卡例外值。亚纯函数tan z以±i为皮卡例外值，外尔斯特拉斯椭圆函数P(z)无皮卡例外值。

人物简介法图是法国数学家。生于洛里昂(Lorient)，卒于波尔尼谢(Pornichet)。1898年就学于高等师范学校。1907年获博士学位。长期在巴黎天文台供职。对泰勒级数、复变量有理函数(亚纯函数)、勒贝格积分(1906)等方面的问题有论述，得到勒贝格积分的一些基本结果。在天文学上用概率方法对恒星与行星的位置测定、双星测量、天文仪器常数等进行过研究。

就学于巴黎高等师范学校 (1898— 1901)，获博士学位(1907)。在巴黎天文台研究应用天文学。在恒星和行星的实际位置、相似恒星检测方面亦做了数学探索。在泰勒级数上亦有重要贡献。3