拟周期函数(quasi-periodic function)是一种特殊的概周期函数,是周期函数的推广,两个周期函数叠加后不产生新的周期函数,这样的函数叫做拟周期函数。“拟周期”概念的提出来自应用科学,比如在晶体理论和力学乃至混沌研究中都有应用。但在数学中没有必要建立相应理论,因为只要分别对各周期函数项研究清楚就行了。
基本介绍拟周期函数(quasi-periodic function,也称殆周期函数),是周期函数的一种推广,是具有某种近似周期性的有界连续函数。其数学描述如下:
对于函数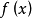 ,设有常数
,设有常数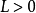 和C,使得
和C,使得
 则称
则称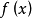 为拟周期函数,L称为函数
为拟周期函数,L称为函数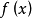 的周期,C称为函数
的周期,C称为函数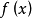 相应于L的周期增量,或简称为周期增量。拟周期函数有无穷多个周期与周期增量。如果它有最小的正周期,则称这个最小正周期为这个拟周期函数的主周期,相应的周期增量称为主周期增量。
相应于L的周期增量,或简称为周期增量。拟周期函数有无穷多个周期与周期增量。如果它有最小的正周期,则称这个最小正周期为这个拟周期函数的主周期,相应的周期增量称为主周期增量。
容易证明:
①周期函数是拟周期的;
②周期函数必是概周期的;
③拟周期函数必是概周期函数。
可见,拟周期函数是周期函数的推广,是概周期函数的特殊情况1。
相关性质拟周期函数是在研究周期函数某种性质的基础上进一步提出来的。三角多项式以及三角多项式序列的极限都是周期函数,而三角和
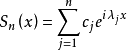 (其中,
(其中,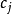 为复数,
为复数,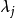 为实数)序列的极限却未必是周期函数。但这类极限函数的特征可以用某种近似周期性来刻画。
为实数)序列的极限却未必是周期函数。但这类极限函数的特征可以用某种近似周期性来刻画。
考虑最简单的情形,设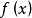 和
和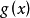 为连续周期函数,
为连续周期函数,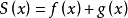 ,设F为
,设F为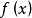 的周期,G为
的周期,G为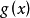 的周期。如果F和G是可公度的。即存在正整数
的周期。如果F和G是可公度的。即存在正整数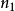 和
和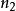 ,使得
,使得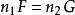 ,那么
,那么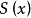 也为一周期函数,而且以
也为一周期函数,而且以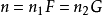 为周期。但当F和G是不可公度时,虽然不存在整数
为周期。但当F和G是不可公度时,虽然不存在整数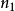 和
和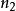 ,满足
,满足
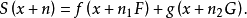 但由有理数集的稠密性原理可知:存在正整数
但由有理数集的稠密性原理可知:存在正整数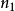 和
和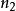 ,满足
,满足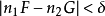 ,这里,
,这里,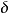 是事先任给的正数。从而存在数
是事先任给的正数。从而存在数 满足
满足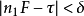 和
和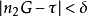 。
。
还可以进一步证明更强的结论:对任给的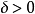 ,存在着正数
,存在着正数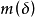 ,使得在每一个长为
,使得在每一个长为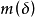 的区间内至少有一数
的区间内至少有一数 满足上式。这样,由
满足上式。这样,由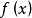 和
和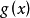 的连续性、周期性以及上述事实便得到:对任给的
的连续性、周期性以及上述事实便得到:对任给的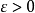 存在着正数
存在着正数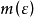 ,使得在每一个长为
,使得在每一个长为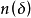 的区间内至少有一数
的区间内至少有一数 ,满足
,满足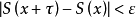 。
。
上式虽然并不能说明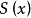 为周期函数,但它具有近似的周期性。一般来说,可以给出如下的精确描述:设
为周期函数,但它具有近似的周期性。一般来说,可以给出如下的精确描述:设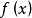 为定义于实轴上的复值连续函数,如果
为定义于实轴上的复值连续函数,如果 满足
满足
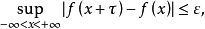 就称
就称 为的
为的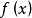 属于
属于 的平移数。若对任意
的平移数。若对任意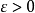 ,存在
,存在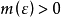 ,使得长度为
,使得长度为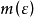 的区间内至少包含一个
的区间内至少包含一个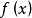 的属于
的属于 的平移数,则称
的平移数,则称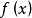 为拟周期函数。
为拟周期函数。
由上可知,任意有限个****周期函数的和函数也必为拟周期函数。复值三角和必为拟周期函数。拟周期函数理论中的一个重要结果是: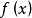 为拟周期函数当且仅当
为拟周期函数当且仅当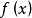 可以用上述的三角和序列
可以用上述的三角和序列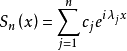 来一致逼近。
来一致逼近。
由确定性微分方程描述的非线性动力学系统具有多种定态运动形式,其中平衡点、周期性(包括谐波、次谐波)、拟周期(或准周期)性、概周期和混沌运动等已为人们所认识。为了全面地揭示动力学系统的行为特征,需要借助于相空间和参数空问。上述运动形式在相空间中由其相应的轨线(例如分别由不动点、闭轨线、环面和奇异吸引子等)描述,在参数空间中,当系统参数在大范围变化时,则由其相应的分支点(bifurcation point)、频率捕捉区域(entrainment regions)表征。系统的相空间一般由其状态变量构成,而参数空间则反映着一个系统所处的外部环境,它与外界的能量、信息和物质的交换都是通过其相应的参数实现的,所以对远离平衡的耗散动力学系统而言,其参数空间是必不可少的。作为显示系统中某个物理变量的具体方法,往往观察其时间波形和功率谱的分布形式(分离或连续的)。物质总是以某种运动形式存在的,一个系统的整体行为特征一般可通过某种变量反映出来,而且它的各种运动形式之间存在着内部联系。作为一种复杂的运动形式,混沌状态的时间波形是非周期的,功率谱是宽带连续的,轨线具有奇异吸引子结构。在一定条件下,通过调节适当的参数,系统可通过周期分支、拟周期运动等到达混沌。目前倍周期分支和切分支到达混沌的研究,已有大量的理论和实验结果,关于拟周期运动及其向混沌的转化在理论和数值模拟方面也有较多论证。作为介于周期与非周期之间的一种运动形式,拟周期状态在动力学系统理论中并非新概念,然而要在物理实验中正确识别并获得这种状态是困难的,也就是说,令人信服的物理实验证实尚为数不多1。
拟周期信号拟周期信号(或波形)可表示为多种周期函数叠加的形式:
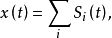 其中
其中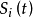 具有最小周期
具有最小周期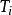 ,频率为
,频率为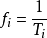 ,而且各个
,而且各个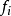 之间不可公度。另外,存在着一个有限的基本频率集合
之间不可公度。另外,存在着一个有限的基本频率集合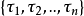 ,它具有这样的性质:
,它具有这样的性质:
(1)它是线性独立的,即不存在任何一个非零整数集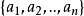 ,使得
,使得
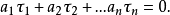
(2)它构成一个完全有限频率基,总能找到某些非零整数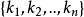 ,使得对于每个
,使得对于每个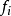 ,有
,有
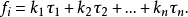
通常把具有n个基本频率的拟周期信号称做n-拟周期的。当然,当n=1时,拟周期信号就是一个周期波形。最简单的2-拟周期波形为
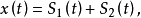 其中
其中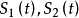 的周期分别为
的周期分别为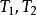 ,而且
,而且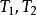 是互不公度的(incommensurable)。
是互不公度的(incommensurable)。
一个常见的例子就是调相信号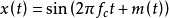 。如果m(t)的基本频率为
。如果m(t)的基本频率为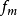 ,则
,则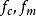 互不公度时,
互不公度时,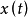 是具有基本频率集合
是具有基本频率集合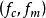 的2拟周期波形1。
的2拟周期波形1。
本词条内容贡献者为:
尚华娟 - 副教授 - 上海财经大学




 扫码下载APP
扫码下载APP

 科普中国APP
科普中国APP
 科普中国
科普中国
 科普中国
科普中国