[科普中国]-力迫条件

基本介绍

力迫条件(forcing condition)是公理集合论术语，指用于力迫构造的偏序集的元素。美国数学家科恩(P.J.Cohen)对力迫条件的原始定义形为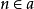或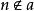的有限协调公式集，这里a代表用于兼纳扩充的兼纳集(或代表兼纳集的名)，n为自然数。因此，每个力迫条件就给出了兼纳集元素构成的一个局部情况，由于兼纳扩充模型由兼纳集G所决定，因此，一定的力迫条件可以确定出兼纳模型中具有或者不具有某种性质，一列适当的力迫条件无穷序列可以确定出兼纳扩充中的所有性质，这种力迫条件序列称为完备力迫条件序列。现代力迫法对力迫条件的定义由科恩的原始定义抽象与简化而得。

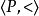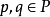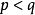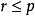设为用于力迫构造的偏序集，为两个力迫条件，若，则称p强于q，若存在使且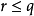，则称p与q相容，否则称为不相容，记为。

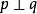力迫法力迫法(forcing method)是构造集合论模型的主要方法之一，它是由美国数学家科恩(P.J.Cohen)于1963年为证明连续统假设的否定(ᒣCH)与ZFC公理系统的相容性、选择公理的否定(ᒣAC)与ZF公理系统的相对相容性时发明的，构造集合论模型主要有两条途径：一是内模型方法，即从ZF(C)系统的一个模型M出发，构造M的一个子模型N，使N为ZF(C)∪{φ}的模型。美籍奥地利数学家哥德尔在证明CH及AC的相容性时采用的即是内模型法；二是外模型法，即从ZF(C)系统的一个模型M出发，通过扩充M成为一个更大的模型N，使N为ZF(C)∪{φ}的模型。科恩通过分析哥德尔的证明过程意识到，要证明ᒣCH及ᒣAC的相对相容性，至少不可能在已有的ZF(C)系统的标准模型之内构造一个标准模型，使之满足ᒣCH或ᒣAC。因此，他采用了外模型方法。假设ZF(C)系统有一个可数的可传标准模型M，取不属于M的自然数集合a(因M可数，故这样的a不仅能找到，而且很多)，把a加到M上，以扩充出一个新的模型N[a](⊇M∪{a})，使得N[a]满足M所满足的ZF(C)系统的所有公理。为此，必须恰当选择a，以“逼迫”(Forcing)N[a]满足人们所希望的命题。这一过程有些像代数中构造代数扩域的过程，将a作为一个待定元，通过观察N[a]的性质确定a。由于a为自然数集合，因此a的性质取决于哪些自然数属于它，哪些自然数不属于它。设p为ω到{0，1}的有限函数，用函数p来表示a的一个部分信息，即当p(n)=1时，表示n∈a；当p(n)=0时，表示n∉a。如果能凭借a的一个部分信息p推知N[a]必定满足某个集合论性质A，则称p“力迫”A在N[a]中成立，记为p⊨A，这里p称为力迫条件，A称为力迫结论，“力迫”一词的含义是因为a具有条件p之后，才迫使性质A在N[a]中成立，通过恰当定义力迫关系“⊨”，可以使之满足下列性质：

1.可靠性：p⊨A与p⊨TA不能同时成立；

2.平凡性：若p⊨A，则对任何q⊇p，q⊨A(因为q比p包含了更多有关a的信息)；

3.完全性：对任何条件p及性质A，总存在条件q⊇p，使q⊨A或⊨ᒣTA，此时称q决定A。

根据上列性质，先将所有集合论性质排成一个序列A0，A1，…，任取一个力迫条件p作为起点，若p不能决定A0，则由完全性可知存在p0⊇p，使p0决定A，否则取p0=p。若p0也能决定A1，则取p1=p0，否则取p1⊃p0，使p1决定A1，依此类推，可以得到一个力迫条件序列{pn}，使得对任何n，pn⊨An或pn⊨ᒣAC，称这样的序列为一个完全序列，它完全决定了N[a]的性质，令a={n：pn(n)=1}，从而待定元a就可以由力迫序列{pn}所确定，一个实际的力迫证明通常采用反证法，它是一种对角线方法，对给定的力迫序列{pn}，若欲证明性质A在N[a]中成立，反证假设ᒣA在N[a]中成立，从而存在一个力迫条件pn⊨TAn，因pn有限，故可对pn进行恰当扩充，使q⊃pn且q⊨ᒣ(ᒣA)，但由性质2，q⊨ᒣA，这与性质1矛盾，从而得出原证结论。利用这种方法可以证明ZFC+V≠L相对于ZFC系统相容。对上列方法再进行一般化，可以证出ᒣAC，ᒣCH的相容性结果。

以上为科恩的力迫法的基本思想，在随后的十多年中，人们对力迫法作了较大的改进，形成了多种力迫法表述形式，最有代表性的是斯科特(Scott，D.S.)与以色列学者索洛韦(Solovay，R.M.)等人发展的布尔值模型方法及休恩菲尔德(Shoenfield，J.R.)给出的偏序集上的兼纳扩充方法。目前通常采用后一种表述方法或将两种方法相结合。力迫扩张的过程可大致描述如下：对ZF(C)系统的一个可数可传模型M(称为基模型)以及M中的一个偏序P(称为力迫概念)，令G⊆P为P的一个兼纳子集(参见“兼纳集”)，一般地，G∉M，由兼纳模型定理(参见“兼纳模型定理”)，存在一个包含G且扩充M的模型M[G]，使M[G]为ZF(C)系统的一个可数可传模型。M[G]称为M的兼纳扩充。为了能在基模型M中讨论扩充模型M[G]的性质，引入若干新的常元(它们可以在M中定义出来)，用以表示M[G]中的集合，通常称之为M[G]中元素的名，记为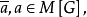借助这些名，可以在基模型中描述兼纳模型M[G]的性质。

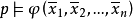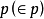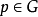在基模型中，恰当定义力迫法关系(这里称为力迫条件，φ为经扩充的集合论语言的公式，为的名)，使得如下力迫定理成立：当且仅当存在，使。因此，M[G]的性质就可以由M中的力迫关系所决定。为了证明某个集合论假设A加到ZF(C)系统后相对ZF(C)系统的相容性，可以适当构造偏序集P，使得兼纳扩充M[G]满足A。利用这种方法可获得诸如ZFC+ᒣCH，ZF+ᒣAC，ZFC+GCH+V≠L等相对相容性结果。如果进行一次力迫扩充，仍不能使兼纳扩充模型获得所需的性质，可以将扩充后的模型作为基模型，再进行若干次扩充，直至获得所需的性质。这种方法称为迭代力迫法。例如ZFC+MA+ᒣCH以及ZFC+SH的相对相容性即是用迭代力迫法获得证明的。近十多年来，应用迭代力迫法进行了大量的研究，取得了非常丰富的研究成果。以色列数学家谢拉赫(S.Shelah)在这方面的成就举世瞩目。他引入正常力迫法并且证明了许多迭代力迫法的保持定理，谢拉赫还用他的理论解决了一大批著名的数学问题，如拓扑学中的P点存在性问题，无限交换群中的怀特海问题等，目前已被应用于递归论、超限算术、无穷组合论、一般拓扑、测度论、泛代数、模型论等众多领域，是迄今为止获得相对相容性结果的主要方法1。