[科普中国]-霍普夫代数同态

概念介绍

霍普夫代数同态(Hopf algebra homomor-phism)是指满足特定条件的双代数同态。设(H，μ，η，Δ，ε，S)和(H′，μ′，η′，Δ′，ε′，S′)是R上的两个霍普夫代数。若f是(H，μ，η，Δ，ε)到(H′，μ′，η′，Δ′，ε′)的一个双代数同态，并且S′·f=f·S，则f称为霍普夫代数同态。1

霍普夫代数20世纪60年代以后迅速发展起来的代数学的新学科。域k上的霍普夫代数是同时具有k代数结构和它的对偶结构(k余代数结构)并满足一定的相容条件的代数系统。霍普夫代数理论的发展有两个来源.一个来源是代数拓扑学，这方面的工作可以追溯到霍普夫(Hopf，H.)于1941年关于系统在域k中的连通李群G的上同调群H(G，k)的研究.霍普夫得到一个十分卓越的结果：当k是特征为0的域时，H(G，k)是具有奇数阶生成子的外代数且其维数是有限的。后来博雷尔(Borel，A.)于1953年、米尔诺和穆尔(Milnor，J.W.-Moore，J.C.)于1965年又做了重要的推广和深化(如把连通李群推广到道路的H空间和与之对偶的同调群即邦德列雅金(Pontrygin)代数H*(G，k)的研究等)，这方面的工作导致了分次霍普夫代数理论，这也是其命名的由来。另一个来源是表示理论，开始于霍赫希尔德(Hochschild，G.)和莫斯托夫(Mostow，H.)于1957年对李群的表示环的研究。史维德勒(Sweedler，M.E.)沿着这个方向建立了非分次的霍普夫代数理论，推动了霍普夫代数的迅速发展。分次的与非分次的霍普夫代数虽然结构相似，却是题材互异。

霍普夫代数的结构从对偶的角度看可说是十分自然的。例如把上文述及的G取为有限群，就可以得到群代数及其对偶代数作为霍普夫代数的平凡例子。G也可以取为拓扑群、代数群等，因此，在数学的许多分支中都存在着具有霍普夫代数结构的对象。霍普夫代数理论在许多数学分支中都有重要的应用，例如代数群理论、域扩张的伽罗瓦理论和布饶尔群理论、C代数、李代数和李超代数、组合理论等。

霍普夫代数在物理学中的模型是量子群，因此它在物理学，特别是量子逆扩散方法和超对称理论的研究中，占有显著的重要地位。

在霍普夫代数的以下诸词条中，若没有特别说明，则R恒指有单位元的交换环，所有R上的代数均指有单位元的结合代数。2

人物简介霍普夫是瑞士数学家.生于德国的布雷斯劳(今波兰弗罗茨瓦夫)，卒于瑞士措刊孔。早年就学于柏林大学、海德堡大学。1925年获柏林大学博士学位，同年又到格丁根大学学习1927—1928年，在普林斯顿大学做研究工作.1931年被聘为瑞士苏黎世高等工业学院教授，直至1965年退休。美国全国科学院和意大利林琴科学院外籍院士.1955—1958年任国际数学联盟主席。

霍普夫的工作很大一部分与代数拓扑有关。他在20世纪30年代的工作是后来的球同伦研究的先驱。在柏林大学时，他证明了布劳威尔映射度是映射S→S的惟一同伦不变量，得到了布劳威尔-霍普夫定理。1925年到格丁根后，受诺特(Noether，E.)影响较大，他第一个把诺特的概念框架应用于同调论，证明了欧拉-庞加莱公式的推广。1931年，他证明了存在映射f：S→S，f被称为霍普夫映射，也就是著名的霍普夫纤维化或主霍普夫丛.这在同伦论发展史上具有重要意义.他还定义了霍普夫不变量，并证明了上面映射的不变量为1.1935年，他又推广了上面映射，得到了映射f：S→S，并对这种映射进行了同伦分类，证明了当n=4，8时，所有映射不变量相等.后被人证明，当n=2，4，8时，霍普夫不变量都为1。这时映射就成为以S为全空间，以S为底空间的纤维丛的映射。他首次证明了本质，但是零调的映射的存在性，且基本性质不能用诱导同调同态来检验。1941年，他建立了H空间，并在研究H空间的同调以及上同调时，又建立了霍普夫代数。现在霍普夫代数已是现代代数的一个重要组成部分，并是代数拓扑学的常用工具。此外，他在拓扑和微分几何的其他很多方面也做出了重要贡献。他曾和亚历山德罗夫(Александров，А.Д.)进行过长期的合作，1935年，他俩合著的《拓扑Ⅰ》一书，对拓扑学的发展起了很大的推动作用.1969年，他还获国际罗巴切夫斯基数学奖。他的主要论著均收入了他1964年出版的《文选》中。

双代数一种代数系统。它既有代数结构，又有余代数结构，且两种结构具相容性。设(B，μ，η)是R代数，且(B，Δ，ε)是R上的余代数，其中μ是B的乘法映射，η是刻画B的单位元的映射。若Δ和ε都是R代数同态(等价于μ，η都是R余代数同态)，则(B，μ，η，Δ，ε)称为R上的双代数。3

同态设E与F为两个群胚，它们的合成法则分别记为⊥与⊤。 称从E到F中的映射f是群胚同态，如果对于E的任一元素偶(x，y)，有：

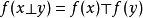设E与F为两个幺半群(两个群)，称从E到F中的映射。f是幺半群(群)的同态，如果f是群胚的同态，且E的中性元素的象是F的中性元素。 (在群的情况下，后一个条件是自然满足的，但是从加法幺半群N到乘法幺半群N的映射x↦0是群胚的同态， 而并不因此就是幺半群的同态)。

设G为乘法群，而a为G的元素。由关系f(n)=an所定义的从加法群Z到G中的映射f是群的同态。

设A与B为两个环(两个体)，称从A到B中的映射f是环(体)的同态，如果f是加法群的同态，且为乘法么半群的同态. 这就是说，对A的任一元素偶(x，y)，有：

f(x+y)=f(x)+f(y)f(xy)=f(x)f(y)，

并且f将A的单位元变成B的单位元。

例如，设n为非零自然数；使任一有理整数对应其对模n的剩余类映射是从环Z到环Z/nZ上的同态。设E与F为两个A-代数(两个酉A-代数)。 称从E到F中的映射f是A-代数(酉A-代数)的同态，如果它是线性映射，并且是乘法群胚(乘法幺半群)的同态。

例如，设E为交换体K上的非零有限n维向量空间，而B为E的基。则从E的全体自同态之酉代数ℒ(E)到K中元素构成的全体n阶方阵之酉代数Mn (K)中的映射，如果该映射使E的任一自同态对应它在基B中的矩阵，则这一映射是酉代数的同态。

同态的概念能用抽象的方式加以推广。4

双代数同态双代数同态是具有双重同态性质的映射。设B和B′是R上的两个双代数，若一个B到B′的代数同态f同时又是余代数同态，则f称为B到B′的一个双代数同态。