[科普中国]-强横截条件

强横截条件亦称几何式横截条件，结构稳定系统的基本条件之一。微分动力系统的研究指出：若系统满足公理 A 和强横截条件，则系统是结构稳定的。人们通常把这类系统称为是公理A结构稳定系统。现已得到对微分同胚和向量场，结构稳定系统等价于公理A结构稳定系统。

简介强横截条件是在公理 A 条件下为保证结构稳定性而进一步提出的一个条件。这个概念在流和离散系统中形式上平行地出现，这里就离散情形加以说明。在公理 A 条件下，流形 M 的每个点正向都趋向某个基本集，实际上与基本集中的某个点正向渐近，即共处于同一稳定流形之中。负向也如此。因此，在公理 A 条件下，M 的每个点x 的稳定流形 Ws(x) 和不稳定流形Wu(x)都是可微的浸入子流形。

如果对任意两点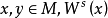 和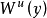 作为可微子流形横截相交，称一个公理 A 微分同胚满足强横截条件。

罗宾(J.Robbin) 和鲁宾逊(R.C.Robinson) 证明，一个微分同胚如果满足公理 A 和强横截条件，则是结构稳定的。这是20世纪70年代微分动力系统的一个主要成果。1

公理A这是斯梅尔为刻画结构稳定性提出的一种关于非游荡集的条件。这个概念在流和离散系统中形式上平行地出现，但由于基础是双曲集的概念，实际上蕴涵着重要的不同。这里就离散情形加以说明。

称一个微分同胚f满足公理 A，如果非游荡集Ω(f) 为双曲集，并且周期点在Ω(f) 中稠密。公理 A 微分同胚的特征是，非游荡集分解成有限个互不相交的拓扑传递的[双曲]紧不变集，称作基本集。

一个微分同胚的动力性态主要体现在非游荡集上，或更大一点，链回归集上。至于游荡部分，或非链回归部分，则比较简单。链回归分解为互不相交的、不可分解的紧不变集，称为链传递分支。一个链传递分支本身可能有复杂的动力形态。但造成动力形态高度复杂的一个更为严重的原因是，一个微分同胚可能有，甚至可能在扰动下持续地有，无穷多个链传递分支。

相比之下，公理 A 微分同胚由于只有有限个链传递分支，动力形态就相对简单（即使各个链传递分支内部可能有斯梅尔马蹄那样的复杂程度）。如果把马蹄这样的不变集看成是一个复杂化了的“鞍点”，把双曲吸引子和排斥子看成是一个复杂化了的“汇点”和“源点”，那么公理 A 微分同胚就在更高的复杂度下类比于一个莫尔斯-斯梅尔微分同胚。

在公理 A 的条件基础上，再加上无环条件或强横截条件，就是斯梅尔提出的、后来被证明为Ω 稳定和结构稳定的充分条件。

本词条内容贡献者为:

尚华娟 - 副教授 - 上海财经大学