[科普中国]-偏差变元微分方程

设t是微分方程的自变元，若方程的未知函数中出现不同于t但依赖于t的变元，则称它为具有偏差变元的微分方程。

简介偏差变元微分方程是泛函微分方程的另一种称谓。

设t是微分方程的自变元，若方程的未知函数中出现不同于t但依赖于t的变元，则称它为具有偏差变元的微分方程。

形式这种不同于t的变元有两种形式：

1.它可以写成g(t)=t-τ(t)，此时τ(t)称为偏差，它甚至可能依赖于未知函数及其导数；

2.它以分布的形式包含在积分号之下，例如方程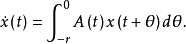已知的各类泛函微分方程都具备这一特点，所以它是经典意义下泛函微分方程的同义语。1

泛函微分方程(functional differential equation)

泛函微分方程是带有各种滞后量的微分方程(微分差分方程)、各种具有复杂变元的微分方程、带有滞后量的积分微分方程等一类方程的概括和抽象。

早在1750年欧拉所提出来的“求一曲线使之与其渐缩线相似”的问题就属于最早的泛函微分方程问题，所求的曲线就满足一个特殊的泛函微分方程。以后在各个学科中不断地提出相类似的问题，因此对泛函微分方程的研究具有重要的实际意义。

本词条内容贡献者为:

胡启洲 - 副教授 - 南京理工大学