全局渐近稳定性(global asymptotic stability)是指一类全相空间均为吸引区域的渐近稳定性。对于线性系统而言,一个线性系统如果是渐近稳定的,则必然是全局渐近稳定的。
总体介绍全局渐近稳定性是一类全相空间均为吸引区域的渐近稳定性。考虑微分方程组
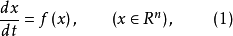 其中
其中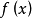 在域
在域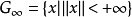 上定义且连续并满足局部李普希茨条件,同时设
上定义且连续并满足局部李普希茨条件,同时设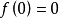 ,因此,对任何初始值
,因此,对任何初始值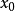 ,存在(1)的惟一的解
,存在(1)的惟一的解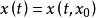 满足
满足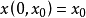 。由李亚普诺夫第二方法知道,如果存在一个定正函数
。由李亚普诺夫第二方法知道,如果存在一个定正函数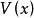 ,它关于(1)的导数
,它关于(1)的导数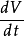 是定负的,那么,方程(1)的奇点
是定负的,那么,方程(1)的奇点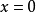 是渐近稳定的,方程组(1)的奇点
是渐近稳定的,方程组(1)的奇点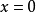 的吸引区域(或称渐近稳定性区域)是所有具有性质
的吸引区域(或称渐近稳定性区域)是所有具有性质
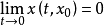 的点
的点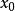 的集合。如果吸引区域是整个相空间
的集合。如果吸引区域是整个相空间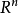 ,则
,则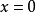 被称为全局渐近稳定的,这时下面的结论成立:如果存在定正函数
被称为全局渐近稳定的,这时下面的结论成立:如果存在定正函数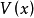 ,它关于(1)的导数
,它关于(1)的导数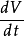 是定负的,并且
是定负的,并且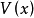 是径向无界的,则奇点
是径向无界的,则奇点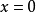 是全局渐近稳定的,李亚普诺夫(А.М.Ляпунов,)原来只考虑原点附近即局部的稳定性,克拉索夫斯基(Н.Н.Красовский)将其推广为全相空间,即全局的稳定性1。
是全局渐近稳定的,李亚普诺夫(А.М.Ляпунов,)原来只考虑原点附近即局部的稳定性,克拉索夫斯基(Н.Н.Красовский)将其推广为全相空间,即全局的稳定性1。
相关概念及定理平衡状态考虑如下非线性动态系统(可以是控制量保持不变的被控对象,也可以是包括被控对象和控制器在内的闭环系统)的状态方程
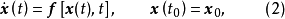 式中,
式中,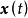 为n维状态向量;
为n维状态向量;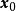 为初始状态;
为初始状态;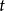 为连续时间变量;
为连续时间变量;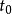 为初始时刻2。
为初始时刻2。
如果状态空间存在某一状态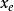 满足
满足
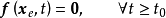 则称
则称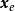 是系统的一个平衡状态,也称平衡点。也就是说,只要无外力作用于系统,存平衡点处系统状态的变化速度为0,系统将永远保持在这个平衡状态上。
是系统的一个平衡状态,也称平衡点。也就是说,只要无外力作用于系统,存平衡点处系统状态的变化速度为0,系统将永远保持在这个平衡状态上。
稳定性如果对于任意给定实数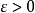 ,存在一个与
,存在一个与 和
和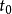 有关的实数
有关的实数 ,只要初始状态
,只要初始状态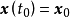 满足
满足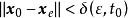 ,系统状态方程式(2)的解
,系统状态方程式(2)的解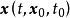 满足
满足
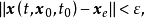 那么,称系统的平衡点
那么,称系统的平衡点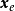 是Lyapunov意义下稳定的。
是Lyapunov意义下稳定的。
注释: 定义中实数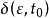 通常有
通常有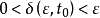 ,定义的直观含义是,在系统受到较小的初始扰动后。系统运动的轨线不会偏离平衡点很远。在二维情况下,设,
,定义的直观含义是,在系统受到较小的初始扰动后。系统运动的轨线不会偏离平衡点很远。在二维情况下,设,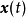 的分量分别是
的分量分别是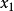 和
和 ,那么在
,那么在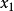 和
和 组成的二维状态空间平面中.状态方程式(2)的解就是起点为
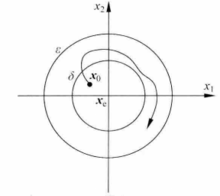
组成的二维状态空间平面中.状态方程式(2)的解就是起点为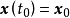 的一条连续的运动轨迹。定义所指的Lyapunov意义下稳定的含义如图1(a)所示。
的一条连续的运动轨迹。定义所指的Lyapunov意义下稳定的含义如图1(a)所示。
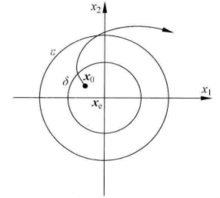
另外,凡是不满足稳定性定义的系统是不稳定系统,其直观意义如图1(d)所示。
渐近稳定性连续时变非线性系统的状态空间模型的一般形式为
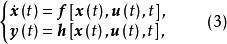 式中,
式中,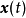 为n维状态变量,
为n维状态变量,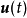 和
和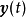 分别为系统的输入和输出向量;t为连续时间变量;
分别为系统的输入和输出向量;t为连续时间变量;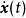 为
为 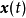 对时间t的一阶导数;
对时间t的一阶导数;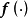 和
和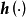 分别为关于
分别为关于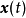 和
和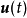 的有界、连续可微的非线性向量函数;n为系统的阶次。
的有界、连续可微的非线性向量函数;n为系统的阶次。
如果式(3)所示动态系统的一个平衡状态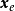 满足
满足
(1) 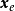 是Lyapunov意义下稳定的;
是Lyapunov意义下稳定的;
(2) 存在一个实数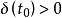 ,使得只要初始状态满足
,使得只要初始状态满足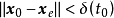 ,就有
,就有
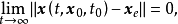 则称
则称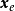 是渐近稳定的。
是渐近稳定的。
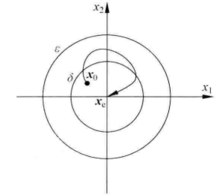
注释: 定义的含义是一切由平衡点的,个小的邻域m发的运动轨线,最终都将收敛到平衡点处,如图1(b)所示。
全局渐近稳定性的意义如果式(3)所示动态系统的一个平衡状态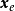 对所有
对所有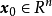 有
有
① 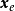 是稳定的;
是稳定的;
② 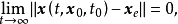 则称
则称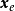 是全局渐近稳定的。
是全局渐近稳定的。
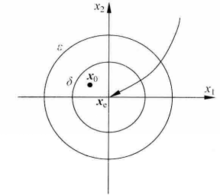
注释: 定义的直观解义如图1(c)所示。对于线性系统而言,一个线性系统如果是渐近稳定的,则必然是全局渐近稳定的。
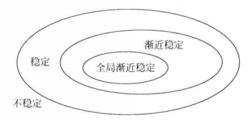
上述各种稳定性定义之间的包含关系如图2所示2。
本词条内容贡献者为:
王海侠 - 副教授 - 南京理工大学




 扫码下载APP
扫码下载APP

 科普中国APP
科普中国APP
 科普中国
科普中国
 科普中国
科普中国