希尔伯特第16问题是著名数学家希尔伯特(Hilbert,D.)提出的涉及平面多项式系统极限环存在和分布问题的重要数学难题。要彻底解决希尔伯特第16问题还有相当大的难度。
简介希尔伯特第16问题是著名数学家希尔伯特(Hilbert,D.)提出的涉及平面多项式系统极限环存在和分布问题的重要数学难题。
发展1900年,希尔伯特在国际数学家大会上提出了23个数学问题,其中第16问题的后半部分是涉及微分方程的,他提出:右端为x,y的n次多项式Pn(x,y),Qn(x,y)的平面系统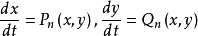 最多有几个极限环,它们的位置分布如何?许多数学家围绕这一问题开展研究,从而深入地推动了平面定性论及一些相关学科分支的研究。
最多有几个极限环,它们的位置分布如何?许多数学家围绕这一问题开展研究,从而深入地推动了平面定性论及一些相关学科分支的研究。
迪拉克(Dulac,H.)于1923年发表长达140页的论文,证明每一确定的系统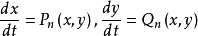 其极限环只有有限个,称之为有限性定理。
其极限环只有有限个,称之为有限性定理。
但后人发现其证明存在缺陷,直至20世纪80年代末期有限性定理才被严格地加以证明,这分别由苏联的依廖申科和法国的埃加勒(Ecalle,J.)、马蒂内(Martinet, J.)等人独立地完成。其核心部分是证明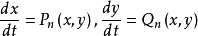 不可能有无限多个极限环聚集在一个分界线环邻近。
不可能有无限多个极限环聚集在一个分界线环邻近。
解决希尔伯特第16问题,人们依不同的n来分别研究系统。n=1时,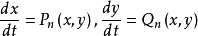 为线性系统,显然不存在极限环。n=2时为二次系统。
为线性系统,显然不存在极限环。n=2时为二次系统。
20世纪50年代起,以叶彦谦和秦元勋为代表的中国数学家对其极限环的基本性质做了系统研究。
至20世纪末在国际上围绕其极限环与全局结构等已有大量成果。鲍金(Bautin,N.N.)证明了二次系统在一个奇点外围邻近最多有三个极限环(1952年)。
20世纪70年代末,史松龄以及陈兰荪、王明淑等给出了具有不少于四个极限环的二次系统(其一个奇点外至少有三个,另一奇点外至少有一个)。
现状至今尚未能证明二次系统最多只能有四个极限环。
对于三次系统(即n=3时)也有不少研究成果,已经获得了如下的实例:在一个奇点外围邻近聚集有8个极限环,也存在三次系统其相互嵌套着的极限环至少有11个。
对n≥4的系统则研究甚少。
总之,要彻底解决希尔伯特第16问题还有相当大的难度。1
本词条内容贡献者为:
胡启洲 - 副教授 - 南京理工大学




 扫码下载APP
扫码下载APP

 科普中国APP
科普中国APP
 科普中国
科普中国
 科普中国
科普中国