[科普中国]-无穷远奇点

无穷远奇点是平面奇点的一种推广，用于研究平面系统的轨线在平面上无穷远处的性态。

简介无穷远奇点是平面奇点的一种推广，用于研究平面系统的轨线在平面上无穷远处的性态。

庞加莱球面庞加莱(Poincare,(J.-)H.)把(x,y)平面上的系统 的轨线投影到与(x,y)平面相切于原点的一个单位球面S上，后人就称此球面S为庞加莱球面。

如下图取坐标系。

在(X,Y,Z)空间中，(x,y)平面上的点M可表示为(x,y,1)。取球心投影，即连结M与球心(0,0,0)，其连线与球面S交于两点，取定下半球面的一点M1(X,Y,Z)。这样就把(x,y)平面上的点一一对应到庞加莱下半球面上，(x,y)平面上的无穷远即对应于S的赤道：X2+Y2=1，Z=0。

为便于写出微分方程研究Z=0上各点邻近的性态，再把下半球面上的点投影到一个适当的铅直平面上。

例如对不是y轴方向的无穷远点，可投影到平面X=1上， 与之相交于点M2，在X=1上取其与球面的切点为坐标原点，u轴与Y轴平行，z轴与Z轴平行，M2的坐标为(u,z)。易推出(x,y)与(u,z)的变换关系为 或 。对y轴方向的无穷远点，则投影到平面Y=1，在其上类似地引进坐标(v,z)，则易得 或 。

在(u,z)坐标下， 变为 z≠0时，此方程组在X=1平面上的轨线为(x,y)平面上 的轨线的投影。而z=0恰好对应于(x,y)面上的无穷元。为消去分母上的z，设P，Q为x，y的多项式，则可将上述方程组写成其中n为非负整数，使，为u，z的多项式且不同时含有因子z。做变换dτ=dt/zn，则化得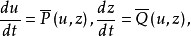它在z=0上的奇点u=u0，z=0称为系统的一个无穷远奇点。

意义通过对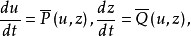的奇点(u0,0)的分析，搞清楚了它的邻域内的轨线的性态，则它的两个半邻域就分别代表了在(x,y)平面上y=u0x方向上的两端无穷远处的轨线性态。1

本词条内容贡献者为:

胡启洲 - 副教授 - 南京理工大学