[科普中国]-正定核

正定核是一类特殊的对称核，其相应的线性积分算子的特征值都是正的。若 K 仅有有限多个负特征值，则称 k(x,y) 必是拟正定核。

定义正定核是一类特殊的对称核，其相应的线性积分算子的特征值都是正的。

设对称核 k(x,y) 是 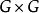上的平方可积函数， K 是以 k(x,y) 为核的线性积分算子。如果 K 作为映 入的算子，其所有的特征值都是正的，则称 k(x,y) 是正定核。

若 K 仅有有限多个负特征值，则称 k(x,y) 必是拟正定核。1

核(kernel)

核是位势论的基本概念。在位势论中，所谓核，常指一般位势的核。

若 恒成立，则称 K 为正核；令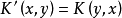（K' 称为 K 的转置核），若 K'=K，则称 K 为对称核；当Ω 为阿贝尔群且有 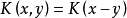时，则称 K 为平移不变核；若对于任意有紧支集的 μ ，有

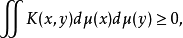则称 K 为正定核，此外，还有各种广义形式的核，如测度核、广义函数核等。

本词条内容贡献者为:

王海侠 - 副教授 - 南京理工大学