[科普中国]-幂级数解法

一阶微分方程的幂级数求解基本方法

求

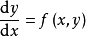满足初始条件 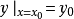的特解，其中

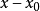我们假设所求的特解可展开成 的幂级数：

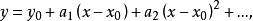其中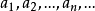， 是待定系数，把上式代入 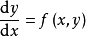中便得一恒等式，比较所得恒等式两端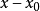的同次幂的系数，就可定出常数 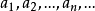，以这些常数为系数的级数在其收敛区间内就是方程 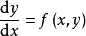满足初始条件 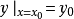的特解。2

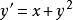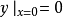例题解析例1 求方程 满足 的特解。3

解 由于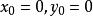 ，故设特解为

把 的幂级数展开式代入原方程，得

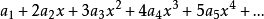
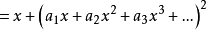
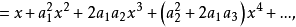比较x同次幂系数，得

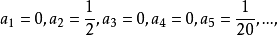故所求解的幂级数展开式的前几项为

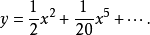
二阶齐次线性方程的幂级数解法定理若方程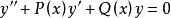 中的系数P(x)与Q(x)可在 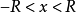内展开为x的幂级数，则原方程必有如下幂级数解

求解方法设解为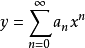，将P(x)，Q(x)，f(x)展开为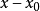的幂级数，比较恒等式两端x的同次幂系数，确定x。2