[科普中国]-扩张定理

扩张定理(extension theorem)是反映正规空间中连续映射的扩张性质的一条定理，是超实数域到超结构的扩张定理1.

定义设 X是度量空间，C 是其闭子空间，则任意C 到R 的连续映射f都可扩张到X 上，即总存在 g:X-R是连续映射，且 g|c=R2。

证明若由M到巴拿赫空间Y的每个有界线性算子T。至少有一在X上的扩张T，即至少存在一个由X到Y的有界线性算子T，当.BEM时T.} -T o.}，使}}TII= II To II，则称Y具有扩张性质3.

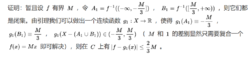
本词条内容贡献者为:

尚华娟 - 副教授 - 上海财经大学