[科普中国]-主理想整环

主理想整环是比单一分解环范围更窄的整环类。若一个环R的任意理想都是主理想，则称R为主理想环。若R同时又为整环，则R称为主理想整环。

整数环Z及域上一元多项式环都是主理想整环，主理想整环必为单一分解环，反之不真。

简介设 R 是一个整环，如果 R 的每个理想都是主理想，即都可以由一个元素生成，则称 R 是主理想整环。

整数环是主理想整环。设 F 是域，则多项式环 F[x] 也是主理想整环。

设 R 是主理想整环，I 是 R 的非零真理想，则

I 是素理想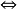I 是极大理想。1

主理想环定义一个整环叫做一个主理想环，假如整环的每一个理想都是一个主理想，则称一个主理想环一定是一个唯一分解环。

等价定义设A为整环，那么下面的条件等价：

1. A是主理想环；

2. A的每个素理想都是主理想；

4. A的任意理想都是主理想；

5. A存在Dedekind–Hasse范数。

整环一个非零环R叫做一个整环（integral domain），整环是抽象代数中最基本的概念之一。对任意的a,b属于环R，假如：

1、乘法适合交换律ab=ba；

2、R有单位元e；

3、R没有零因子ab=0可得a=0或b=0，

则R是整环。

本词条内容贡献者为:

尚华娟 - 副教授 - 上海财经大学