[科普中国]-对称化算子

对称化算子(symmetrization operator)是作用于反对称张量上的算子。张量是向量概念的综合，可用以代表各向量间的关系。例如弹性张量把弹性体上每一点的变形与外加应力联系起来。张量计算最初的发展是与微分几何相联系的，也是爱因斯坦在系统地阐述广义相对论时所用的基本工具。1

概念对称化算子作用于反对称张量上的算子。对任意的x∈Tr(V)，令：

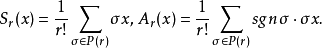它们分别称为r阶反变张量的对称化算子和反对称化算子。用P(V)表示全体对称的r阶反变张量的集合，用Λ(V)表示全体反对称的r阶反变张量的集合。不难验证有性质：Sr°Sr=Sr，Ar°Ar=Ar，且：

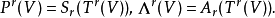这里对于对称张量与反对称张量的讨论同样适用于协变张量。

张量张量是向量概念的综合，可用以代表各向量间的关系。例如弹性张量把弹性体上每一点的变形与外加应力联系起来。张量计算最初的发展是与微分几何相联系的，也是爱因斯坦在系统地阐述广义相对论时所用的基本工具。2

n维空间中的一个量，它具有nr个分量，用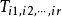表示，它的每个分量都是坐标的函数；在坐标变换下，这些分量按照一定的规律作线性变换。r称为张量的阶。

张量是矢量及矩阵概念的推广。标量是零阶张量;向量是一阶张量；矩阵是二阶张量。三阶张量(它的分量用Tijr表示)就像是一个“立体矩阵”。

在1900年，张量首先在弹性理论中使用。“张量”原来的含义是“张紧”与“张开”。

1892年起，里奇(C.G.Ricci，意，1853—1925)与列维·奇维塔(T.Levi-Civita，意，1873—1941)开始建立张量分析的理论，成为黎曼几何与广义相对论的一种工具。

为了简便，在张量列式或计算时，常按求和约定将求和号略去。

张量空间张量空间(tensor space)是多重线性代数的重要概念，定义是有张映射的一种向量空间。多重线性代数式代数学的一个重要分支。可以将它看做是线性代数的发展。它是伴随着微分几何、现代分析、群表示论、理论物理、量子力学等学科发展起来的，并且在这些学科中已得到重要的应用。具体定义有多种不同的形式。例如，可定义为：设P是一个向量空间，若存在张映射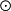：V1×V2×…×Vm→P使得〈Im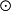〉=P，则称P为V1，V2，…，Vm的带有张映射的张量空间；或称P为V1，V2，…，Vm的张量积空间；或简称P为V1，V2，…，Vm的张量积，记为：

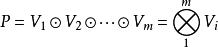张量空间对于多重线性代数的重要性如同向量空间对于线性代数的重要性。张量空间的维数是：

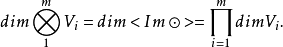
多重线性代数代数学的一个重要分支。可以将它看做是线性代数的发展。它是伴随着微分几何、现代分析、群表示论、理论物理、量子力学等学科发展起来的，并且在这些学科中已得到重要的应用。

多重线性代数形成为一个学科还是近几十年来的事，值得提出的是20世纪50年代，布尔巴基(Bourbaki，N.)论述多重线性代数的书及20世纪60年代，葛瑞布(Greub，W.)的多重线性代数专著(第一版)，特别是从1973年，由马库斯(Marcus，M.)和汤普森(Thompson，R.C.)创办了国际性的《线性和多重线性代数》(Linear and Multilinear Algebra)杂志以及同年马库斯出版了经典性著作《有限维多重线性代数》以来，多重线性代数的发展进入了一个活跃的新阶段，这当中以梅里斯(Merris，R.)等人研究高阶特征标的张量对称类所获得的成果最为突出。

多重线性代数研究的内容包括：多重线性映射、具有一定对称性质的多重线性映射、张量空间、张量对称类、张量代数、对称张量代数、格拉斯曼代数、外代数、克利福德代数及其表示理论等。这里的前半部分只就常用的有限维多重线性代数来叙述，对于以泛性质手段处理的无限维情形可参看葛瑞布(Greub，W.H.)于1978年著的《多重线性代数》(第二版)。对可换环上建立在环模上的多重线性代数则可参看诺茨考特(Northcott，D.G.)于1984年著的《多重线性代数》。

多重线性代数这部分词条的向量空间一般是指一个特征为零的域K上的(向量)空间，但当关系到内积和群的任意特征标时，为了叙述简明则只在复数域C上讨论.域上的多重线性代数的主要概念与结果都可用模论的工具推广到交换环上的多重线性代数，这里不再一一提及。交换环上的多重线性代数在模论、同调代数、代数K理论、代数几何等学科中都有重要应用。3

混合张量混合张量(mixed tensor)是一类张量。向量空间及其对偶空间张量积的元素。张量是向量概念的综合，可用以代表各向量间的关系。例如弹性张量把弹性体上每一点的变形与外加应力联系起来。张量计算最初的发展是与微分几何相联系的，也是爱因斯坦在系统地阐述广义相对论时所用的基本工具。

张量空间：

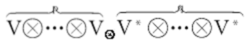
(记为Vq)中的元素称为p重反变q重共变张量；或称为(p，q)重混合张量，其中V是C上向量空间，V*=L(V，C)是V的对偶空间。混合张量也指：

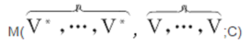
中的多重线性函数。可以定义张映射使：

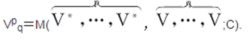
V0中的元素称为反变张量。Vq中的元素称为共变张量。这些都是微分几何、黎曼几何及物理上用得较多的概念。

本词条内容贡献者为:

尚华娟 - 副教授 - 上海财经大学