[科普中国]-自相似测度

自相似测度（self-similar measure）是一类典型而重要的分形测度。它是目前了解得最深入的一种分形测度

简介自相似测度是一类典型而重要的分形测度。

设E压缩比为c1,c2,...,cm的相似压缩族S1,S2,...,Sm生成的自相似集。若P=(p1,p2,…,pm)为一概率向量，即pi>0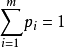，。视p为符号集Ω={1,2,...,m}上的概率测度，满足p(i)=pi，τ为由p诱导的符号空间Ωω上的乘积测度，则存在惟一的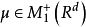满足：

1.；

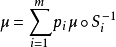2. supp μ=E，其中supp μ为μ的支集，上述测度μ称为由相似压缩族S1,S2,...,Sm概率向量(p1,p2,…,pm)定义的自相似测度。

发展自相似测度由哈钦生(Hutchinson,J.E.)于1981年引入。

它是目前了解得最深入的一种分形测度。1

自相似集自相似集是一类具有自相似性的分形集合，是最重要的分形集类。

设Φ={φ1,φ2,...,φm}为有限压缩族，所有的φj均为相似压缩，则F称为自相似集。它由具有各向同性的线性压缩族，即相似压缩族生成，其最重要的特征是它的局部与整体具有严格的相似。

自相似集在分形几何的研究中具有非常特殊的地位。

本词条内容贡献者为:

胡启洲 - 副教授 - 南京理工大学