定义
广义梯度(generalized gradient)是梯度或导数概念的一种推广,这是克拉克(Clarke,F.H.)对于局部李普希茨函数类提出的概念,由此形成的理论目前已成为非光滑分析中最成熟的一部分,并且有广泛的应用2。
设f(x)在x附近是Lipschitz的,则我们称集合
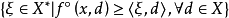 是
是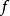 在
在 处的广义梯度,记为
处的广义梯度,记为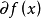 。
。
相关性质共轭空间X*的范数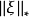 定义为
定义为
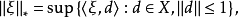 则关于广义梯度有如下结果。
则关于广义梯度有如下结果。
引理1设f(z)在x附近是Lipschitz 的,则
1) 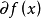 是X* 中的一个弱*—紧的、非空凸集;而且对
是X* 中的一个弱*—紧的、非空凸集;而且对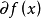 中任何
中任何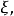 都有
都有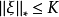 。
。
2) 关系式
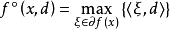 对一切
对一切 都成立。
都成立。
根据定义明显可见广义方向导数和广义梯度有如下关系。
引理2设f(z) 在 x 附近是Lipschitz 的,则
 当且仅当
当且仅当
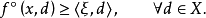
广义梯度对于数乘具有交换性,即对任何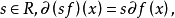 如果
如果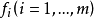 是有限个在 x 附近Lipschitz 的函数,则
是有限个在 x 附近Lipschitz 的函数,则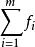 在x附近也是lipschitz 的,而且有关系式
在x附近也是lipschitz 的,而且有关系式
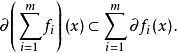 如果
如果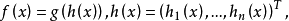 每个
每个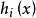 都在x附近是Lipschitz的,
都在x附近是Lipschitz的,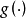 在h(x)附近是Lipschitz的,则f(x)在x 附近是Lipschitz 的且有
在h(x)附近是Lipschitz的,则f(x)在x 附近是Lipschitz 的且有
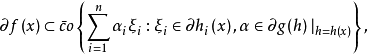 其中
其中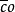 表示弱*- 紧凸包。
表示弱*- 紧凸包。
利用引理2,我们可得到非光滑优化的一阶必要条件:
定理1如果f(z) 在x* 处达到局部极大或局部极小,且f(x) 在x*附近是Lipschitz 的,则必有

关于充分性条件,我们有以下定理。
定理2设f(x) 在X* 附近是凸的和Lipschitz 的,且
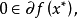 则x* 是f(x)的局部极小点。
则x* 是f(x)的局部极小点。
我们还可得到一个关于严格(强) 极小点的充分性条件。
定理3设f(x) 在x*附近是凸的和Lipschitz 的,如果
 则x* 是f(x)的严格(强)极小点,即存在
则x* 是f(x)的严格(强)极小点,即存在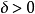 使得
使得
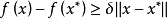 对所有充分靠近x*点处的x 都成立1。
对所有充分靠近x*点处的x 都成立1。




 扫码下载APP
扫码下载APP

 科普中国APP
科普中国APP
 科普中国
科普中国
 科普中国
科普中国