[科普中国]-次微分

次导数（subderivative）、次微分（subdifferential）、**次切线（subtangent lines）和次梯度（subgradient）**的概念出现在凸分析，也就是凸函数的研究中。 要注意的是，次切线（subtangent lines）和次切距（subtangent）是不同的。

定义设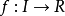是一个实变量凸函数，定义在实数轴上的开区间内。这种函数不一定是处处可导的，例如绝对值函数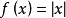。但是，从右面的图中可以看出（也可以严格地证明），对于定义域中的任何x0，我们总可以作出一条直线，它通过点(x0,f(x0))，并且要么接触f的图像，要么在它的下方。这条直线的斜率称为函数的次导数。

凸函数f:I→R在点x0的次导数，是实数c使得：

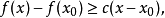对于所有I内的x。我们可以证明，在点x0的次导数的集合是一个非空闭区间[a,b]，其中a和b是单侧极限

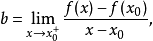它们一定存在，且满足a≤b。

所有次导数的集合[a,b]称为函数f在x0的次微分。1

例子概述考虑凸函数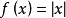。在原点的次微分是区间[−1, 1]。x00，则是单元素集合{1}。

单元素集合数学上，单元素集合是由唯一一个元素组成的集合。例如，集合 {0} 是个单元素集合。注意，集合诸如 {{1,2,3}} 也是单元素集合，唯一的元素是一个集合（这个集合可能本身不是单元素集合）。

一个集合是单元素集合，当且仅当它的势为1。在自然数的集合论定义中，数字 1 就是定义为单元素集合 {0}。

在公理集合论中，单元素集合的存在性是空集公理和对集公理的结果：前者产生了空集{}，后者应用于对集 {} 和 {}，产生了单元素集合 {{}}。

若A是任意集合，S是单元素集合，则存在唯一一个从A到S的函数，该函数将所有A中的元素映射到S的单元素。

在范畴论中，单元素集合上构建的结构通常作为终对象或零对象：

上述说明所有单元素集合S都是集合范畴的终对象。该范畴中没有其它终对象。

任意单元素集合都能够转化成拓扑空间（所有子集都是开集）。这些单元素拓扑空间是拓扑空间范畴的终对象。该范畴中没有其它终对象。

任意单元素集合都能够转化成群（唯一的元素作为单位元）。这些单元素是群范畴的零对象。群范畴中没有其它零对象或终对象。2

性质凸函数在x0可导，当且仅当次微分只由一个点组成，这个点就是函数在x0的导数。

点x0是凸函数f的最小值，当且仅当次微分中包含零，也就是说，在上面的图中，我们可以作一条水平的“次切线”。这个性质是“可导函数在极小值的导数是零”的事实的推广。2

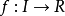
次梯度次导数和次微分的概念可以推广到多元函数。如果是一个实变量凸函数，定义在欧几里得空间R内的凸集，则该空间内的向量v称为函数在点x0的次梯度，如果对于所有U内的x，都有：

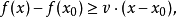所有次梯度的集合称为次微分，记为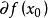。次微分总是非空的凸紧集。

欧几里得空间欧几里得几何是在约公元前300年，由古希腊数学家欧几里得建立的角和空间中距离之间联系的法则。欧几里得首先开发了处理平面上二维物体的“平面几何”，他接着分析三维物体的“立体几何”，所有欧几里得的公理被编排到几何原本。

这些数学空间可以被扩展来应用于任何有限维度，而这种空间叫做n维欧几里得空间（甚至简称n****维空间）或有限维实内积空间。

这些数学空间还可被扩展到任意维的情形，称为实内积空间（不一定完备），希尔伯特空间在高等代数教科书中也被称为欧几里得空间。 为了开发更高维的欧几里得空间，空间的性质必须非常仔细的表达并被扩展到任意维度。 尽管结果的数学非常抽象，它却捕获了我们熟悉的欧几里得空间的根本本质，根本性质是它的平面性。 另存在其他种类的空间，例如球面非欧几里得空间，相对论所描述的四维时空在重力出现的时候也不是欧几里得空间。

紧空间在数学中，如果欧几里得空间R的子集是闭合的并且是有界的，那么称它是紧致的。例如，在R中，闭合单位区间[0, 1]是紧致的，但整数集合Z不是（它不是有界的），半开区间[0, 1)也不是（它不是闭合的）。

更现代的方式是称一个拓扑空间为紧致的，如果它的开覆盖都有有限子覆盖。海涅-博雷尔定理证明了这个定义对欧几里得空间子集等价于“闭合且有界”。

注意：某些作者如布尔巴基使用术语“预紧致”，并把“紧致”保留给是豪斯多夫空间并且“预紧致”的拓扑空间。一个单一的紧致集合有时称为紧统（compactum）。在法语的数学著作中，quasi-compact是指紧致，compact是指紧致且豪斯多夫，不同于英语。3

参见弱导数

弱微分

本词条内容贡献者为:

孙和军 - 副教授 - 南京理工大学