卡拉西奥多里定理断言,n维空间中的凸集中的每一点都可用该集合的不超过n+l个点的凸组合来表示。
简介卡拉西奥多里定理是有限维凸集的表示定理。
该定理断言,n维空间中的凸集中的每一点都可用该集合的不超过n+l个点的凸组合来表示。1
凸集(convex set)
在凸几何中,凸集是在凸组合下闭合的仿射空间的子集。更具体地说,在欧氏空间中,凸集是对于集合内的每一对点,连接该对点的直线段上的每个点也在该集合内。例如,立方体是凸集,但是任何中空的或具有凹痕的例如月牙形都不是凸集。
特别的,凸集,实数R上(或复数C上)的向量空间中,如果集合S中任两点的连线上的点都在S内,则称集合S为凸集。
凸组合凸组合是一类特殊的线性组合,是若干个点的某种特定意义下的非负线性组合。
设向量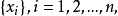 如有实数
如有实数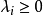 ,且
,且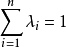 ,则称
,则称 为向量
为向量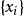 的一个凸组合(凸线性组合)。
的一个凸组合(凸线性组合)。
本词条内容贡献者为:
杜强 - 高级工程师 - 中国科学院工程热物理研究所




 扫码下载APP
扫码下载APP

 科普中国APP
科普中国APP
 科普中国
科普中国
 科普中国
科普中国