[科普中国]-代数边界

代数边界即拓扑学意义下的边界。在拓扑学中，拓扑空间 X 的子集 S 的边界是从 S 和从 S 的外部都可以接近的点的集合。

简介在拓扑学中，拓扑空间X的子集S的边界是从S和从S的外部都可以接近的点的集合。更形式的说，它是S的闭包中的不属于S的内部的点的集合。S的边界的元素叫做S的边界点。集合S的边界的符号包括 bd(S)、fr(S) 和 ∂S。某些作者（比如 Willard 在General Topology中）使用术语“边境”而不用边界来试图避免混淆于代数拓扑学中使用的边界概念。1

S的边界的连通单元叫做S的边界单元。

定义拓扑空间的子集S的边界（记为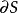 ）有一些常用及等价的定义:

S的闭包减去S的内部：。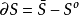

S的闭包和其补集的闭包的交集：。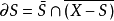

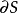是所有满足以下条件的点x的集合：x的每个邻域都包含至少一个点属于S，且至少一个点不属于S。这些点称为S的边界点。

性质集合的边界是闭集。

p是某集合的边界点，当且仅当所有p的邻域包含至少一个点属于该集合且至少一个点不属于该集合。

某集合的边界等于该集合的闭包和该集合的补集的闭包的交集。

某集合是闭集，当且仅当该集合的边界在该集合中；某集合是开集，当且仅当该集合与其边界不相交。

某集合的边界等于其补集的边界。

某集合的闭包等于该集合和其边界的并集。

某集合的边界为空，当且仅当该集合既是开集也是闭集(也就是闭开集)。

举例若 X=[0,5)，则 。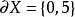

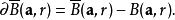
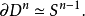
在R中，若 Ω=x+y≤ 1且Z=0，则 ∂Ω = Ω；但在R中，∂Ω = {(x,y) |x+y= 1}。所以，集合的边界依赖其背景空间。

本词条内容贡献者为:

杜强 - 高级工程师 - 中国科学院工程热物理研究所