[科普中国]-仿射包

基本介绍

仿射包(affine hull)是由实线性空间中的集合所生成的仿射集，设A为实线性空间X中的集合，那么包含A的最小仿射集称为A的仿射包。它是所有包含A的仿射集的全体的交集，也是A中的元素的不断用直线连结后的元素全体，A的仿射包通常记为aff A。

仿射包(affine hull )是指由一个点集导出的一类点集。对于En中的子集A，A的仿射包，记为Aff A，为A的任意有限多个元素x1，x2，…，xk的仿射组合

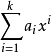构成的集合。一个线性组合

称为仿射组合，若系数αi (i=1，2，…，k)满足

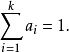当A={x1，x2}时，Aff A为通过x1，x2的直线；当A={x1，x2，x3}时，Aff A为通过x1，x2，x3的平面2。

n 维欧氏空间Rn中的仿射集M 指的是具有x+S 形式的集合，其中x 是某个向量，而S 是由M 唯一确定的一个子空间，并称为平行于M的子空间。换言之，一个集合M 称为是仿射的，如果它包含所有穿过满足x，y∈M 且x≠y 条件的点对x，y 的直线。如果X 是Rn的子集，X 的仿射包(affine hull)，记作aff(X)，是指包含X 的所有仿射集的交集。注意aff(X) 本身是仿射集并且它包含conv(X)，aff(X) 的维数定义为平行于aff(X) 的子空间的维数。可以证明：aff(X)=aff(conv(X))=aff(cl(X))，进而凸集C 的维数定义为它的仿射包aff(C) 的维数。

相关概念凸包令X 为n 维欧氏空间Rn的非空子集，集合X 的凸包(convex hull)，记作conv(X)，是指包含X的所有凸集合的交集，并且该集合是凸集X 的元的凸组合****(convex combination) 是具有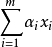 形式的向量，其中m 为正整数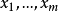， 属于X,而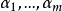 是标量，并满足

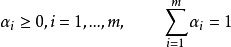条件。注意凸组合属于conv(X) 。对于任意的凸组合以及在conv(X)上为凸的函数 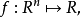我们有

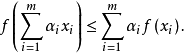这个关系是有名的Jensen 不等式的特例，Jensen 不等式在应用数学和概率论中有着广泛的应用3。

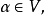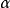仿射集设L是V的一个线性子空间， ,则L沿 的平移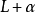 称为V的一个仿射集(affine set)。

仿射集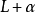 的维数等于线性子空间L的维数，即dim( 。

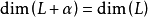设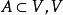中所有包含A的仿射集之交称为A的仿射包(affine hull )，记为aff(A).A的维数定义为aff(A)的维数，即dim(A)=dim(aff( A))4。

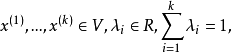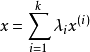仿射组合设称为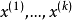的仿射组合4。

相关性质定理定理1设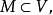 则M是仿射集等价于M包含通过任意两点 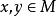的直线，即

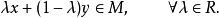
推论1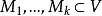 均为仿射集，则交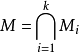集是仿射集。

推论2若M是仿射集，则M必为凸集。

定理2设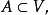则A的仿射包aff(A)等于A 中元素的有限仿射组合的全体4。