[科普中国]-非光滑分析

发展历程

凸分析

研究凸集和凸函数的数学分支.其主要目的在于利用集合和函数的凸性来处理各种分析问题,特别是极值问题,包括有限维的数学规划问题和无限维的变分学问题.其主要工具是凸集分离定理、次微分理论和对偶理论.
凸集的概念可以追溯到公元前3世纪的古希腊时代.当时,阿基米德(Archimedes)已定义凸弧为所有连结其上的点的弦都在同一边的平面曲线.但是系统研究凸集理论是以19世纪末、20世纪初,德国数学家闵科夫斯基(Minkowski,H.)的工作为标志的.闵科夫斯基对凸集的研究兴趣起源于他对“数的几何”问题(例如,一个平面集中至少有多少个坐标为整数的点)的研究.因此,他提出了用来刻画一点到一个凸集距离——而现今称为闵科夫斯基函数的概念,它尤其包括范数、半范数等凸函数作为特例.在他去世后的1911年发表的著作中,他对R中的闭凸集证明了凸集支撑定理.以后,卡拉西奥多里(Carathéodory,C.)等又进一步对凸集理论深入研究,尤其是在1911年提出R中的凸集可用n+1个点来表示的卡拉西奥多里定理.
凸函数概念的系统应用可从柯西(Cauchy,A.-L.)算起.现今,人们熟知的柯西不等式、几何平均不大于算术平均等,都起源于柯西利用函数的凸性来证明不等式的研究.系统的凸性不等式研究是延森(Jensen,J.L.W.V.)的工作,他在1906年发表了这方面的专著.用作凸函数定义的不等式,通常称为延森不等式.
对早期的凸性理论做出重要贡献的还有黑利(Helly,E.).他在1917年证明而在1923年发表的黑利定理指出,如果R中的紧凸集族的任何n+1个集有非空交,那么整个族也有非空交.他甚至还在1921年,比哈恩(Hahn,H.)和巴拿赫(Banach,S.)更早地证明了哈恩-巴拿赫定理;这一涉及凸函数的线性泛函的延拓定理是与凸集支撑定理或凸集分离定理等价的.
20世纪50年代,既由于数学规划、对策论、数理经济学、最优控制等应用数学学科发展的需要,也由于泛函分析、变分学、位势论等基础数学学科发展的需要,凸性的研究变得越来越重要.1951年,芬切尔(Fenchel,W.)在美国普林斯顿大学印发了讲义《凸锥、凸集和凸函数》,对凸集、凸锥和凸函数理论做了系统总结和发展.特别是把变分学中经典的勒让德变换的概念推广成为现今称为勒让德-芬切尔变换或共轭函数的概念,提出上图、指示函数等运用方便的新概念.这些现今在凸分析中都成了基本概念.以后,克利(Klee,V.L.)又在一系列论文中对凸集理论做了深入的剖析.绍凯(Choquet,G.)则发展了1940年提出的克莱因-米尔曼定理(紧凸集是其端点集的闭凸包),而建立了现今的所谓紧凸集和凸锥的绍凯积分表示理论.1911年提出的布劳威尔不动点定理,也在这一时期被发展成为紧凸集中的连续映射的各种不动点定理.其中的代表是角谷静夫1941年提出的紧凸集中的闭集值映射的不动点定理和樊(Ky Fan)从1952年起提出的一系列极小极大不等式.
凸分析真正被认为是相对独立的数学分支,则是由于莫罗(Moreau,J.J.)和洛卡费勒(Rockafellar,R.T.)的工作.1967年莫罗的讲义《凸泛函》和1969年洛卡费勒的专著《凸分析》被认为是凸分析的奠基著作.尤其是其中关于凸函数的次微分理论和对偶理论是使凸分析真正成为分析学科的一部分的标志.莫罗的讲义是在一般的局部凸拓扑线性空间的框架中叙述的,而洛卡费勒则更强调数学规划理论中的应用,把凸分析局限在有限维空间中.以后又陆续出版了艾克兰德(Ekeland,I.)和特曼(Teman,R.)的《凸分析和变分问题》(1974)等旨在针对变分学、最优控制等应用的巴拿赫空间上的凸分析著作.
20世纪70年代以后,凸分析又进一步发展为非凸分析、非光滑分析、集值分析等.许多凸分析的基本定理被推广到非凸集和非凸函数情形.其中最引人注目的是洛卡费勒的学生克拉克(Clarke,F.H.)于1975年提出的关于局部李普希茨函数的广义梯度理论.1994年起,国际上出版了第一本《凸分析杂志》.按照该杂志的发刊词所说,广义的凸分析理论,应包括凸分析的各种推广,尤其是包括非光滑分析、集值分析等.
非凸分析(nonconvex analysis) 试图把凸分析的基本理论和方法推广到非凸集和非凸函数情形的数学分支.这个名称现今已不常用,而代之为非光滑分析、集值分析等。
非光滑分析(nonsmooth analysis) 凸分析的发展.凸分析的次微分理论使得人们能够对非光滑凸函数推广微分法来处理极值问题.非光滑分析就致力于更一般的广义微分法,来处理非光滑函数的极值问题.这方面现今最成功的是克拉克(Clarke,F.H.)对局部李普希茨函数提出的广义梯度理论.他在1983年出版的《最优化和非光滑分析》一书已成为这方面的经典著作。
集值分析(set-valued analysis) 以集值映射为研究对象的数学分析.点对应集合的集值映射是很早就出现的数学概念.但长期来虽有少量研究,却常被人认为不很重要.20世纪50年代以后,由于数理经济学、数学规划理论等的发展,使集值映射概念在其中起本质作用.例如,需求映射、供给映射等作为价格的函数都不是单值的;数学规划问题解的稳定性问题,也涉及解集合(一般的数学规划问题的解没有惟一性)作为参数的集值映射的连续性.凸分析中出现的导数概念的推广——次微分映射也不是单值映射,而是集值映射.这样,就逐渐形成集值分析这个新的分支.1990年,奥邦(Aubin,J.P.)和弗朗科斯卡(Frankowska,H.)出版了《集值分析》一书,初步总结了集值分析的已有成果.1994年,国际上出版了《集值分析杂志》1。

概念体系对于每一种微分和梯度概念，从它的泛函分析和非光滑几何学角度进行归纳与总结，以便建立它们之间的内在联系和数学本质。如表所示，表中的各个概念形成了非光滑分析的体系1。

非光滑分析的概念体系

|| ||

基本概念非光滑分析的基本概念

次微分、Clarke广义梯度、下导数Dˆf(X)和相依上导数D↑f(x；v)分别是凸分析理论、非光滑分析理论、粘性解理论和生存理论中处理非可微函数的重要概念，它们的定义如下1：

(1)次微分af(X)：

假定f(X)为凸函数，则函数在x点的次微分af(X)定义为：

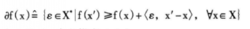
(2)Clarke广义梯度afc(x)：

假定f(x)在x点是Lipsehitz连续的，则函数在x点的Clarke广义梯度afc(X)定义为：

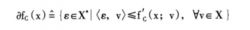
其中f'c(x；v)为Clarke广义方向导数：

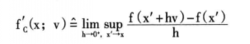
(3)上导数D﹢f(x)和下导数Dˉf(x)：

假定f(x)在X点上可微或下可微，则函数在x点的上导数D+f(x)和下导数Dˉf(x)的定义为：

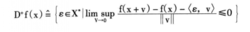
(4)相依上导数D↑f(x；v)和相依下导数D↓f(x；v)

假定f(x)在x点是相依上可导的，则函数在x点的相依上导数D↑f(x；v)和相依下导数D↓f(x；v)分别定义为：

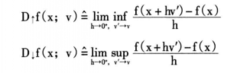
上述微分和梯度的定义方式各不相同，有用线性近似效果定义的，有用对偶集定义的，还有用极限方式定义的。不同的定义方式代表了不同理论背景(泛函分析、凸分析和集值分析等)，虽然它们的描述方式差别很大，但它们之间是有内在联系的(Clarke，1983；Aubin，1990；王春峰，1994；Frankowska，1989，1993)。

在凸分析中，对于凸函数，设方向导数

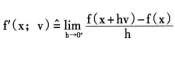
则次微分有如下性质：

(1)v→f’(x；v)是正齐次，次可加凸函数。

(2)式：

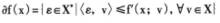
表明方向导数是次微分的支撑函数。

(3)af(·)是非空凸紧集。

由上可知，正齐次、次可加的方向导数v→f’(x；v)控制着一个线性泛函集——次梯度集(这正是著名的Hahn—Banach定理的结论)。非光滑分析正是利用此特性来定义多种广义梯度的。对于一般非光滑函数，方向导数v→f’(x；v)不是凸的，这时应首先凸化方向导数，得到一个正齐次、次可加的凸函数——广义方向导数，然后定义出其对偶集——广义梯度。Clarke广义方向导数和Clarke广义梯度就是用这种方式定义的。相依上导数也可以用这种方式定义相依次微分的概念。

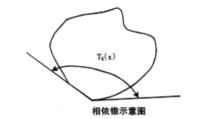
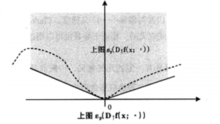
上述的方向导数都具有一定的几何意义，一般都是用函数上图和切锥描述的。上图的作用是将函数概念转换成集合概念。在一定条件下，方向导数的上图是函数上图的切锥，这种几何解释不仅使各种方向导数和广义梯度的含义更加直观，还可以重新定义广义梯度概念。事实上，生存理论中的相依上导数就是用这种方式得到的。相依锥是切锥概念的推广，K集合在x点的相依锥Tk(x)可用集合上极限定义为：

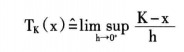
如图所示，它是集合K在x点的一种“内方向”集合。相依上导数的几何解释就是：相依上导数的上图是函数上图的相依锥。

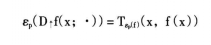
非光滑分析的基本概念间有如下关系：

(1)不可微函数的各种广义导函数都是正齐次泛函，它们的上图是各类几何锥体。当导函数为正齐次、次可加泛函(又称次线性泛函)时，这些锥是凸锥，在集值分析中有很好的性质。同时根据Hahn—Banach定理，x上的次线性泛函控制着X上的线性泛函(ε，v)≤f’(x；v)，即次微分。由此定义的对偶集都是闭凸集，便于利用成熟的凸分析优化技术。

(2)当函数f(x)是F可微函数时，所有上述广义方向导数都等于(f’(x)，v)，其中f’(x)是x点的Frenchet导数，上图的各种切锥都扩展成f’(x)在x点的切平面、切空间，所有的各种广义导数次微分都变成单点梯度集且等于Frenchet导数f'(x)。

(3)当函数f(X)是凸函数时，所有上述广义方向导数都等于X点的方向导

数，各种切锥都成为凸分析中的闭凸切锥，所有的广义导数次微分梯度都等于凸

分析中的次微分。

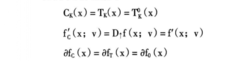
(4)当函数f(X)是上柔滑函数时，相依锥与Clarke相依锥、相依上导数与

Clarke广义方向导数、相依次微分与Clarke广义梯度的关系如下(Aubin，1990)1：