[科普中国]-非线性位势论

非线性位势论是关联于某个从RN到RN的非线性微分算子的位势理论。

简介非线性位势论是关联于某个从RN到RN的非线性微分算子的位势理论。

通常考虑与下面拟线性微分方程▽·(|▽u|p-2▽u)=0相关联的理论，故亦称拟线性位势论。1

线性微分算子微分算子是一类常见而又重要的算子。它是微分方程中研究的核心对象。

设A是由某函数空间E1到函数空间E2的映射，f=Au(u∈E1,f∈E2)。如果像f在每个点x处的值f(x)由原像u和它的某些导函数在x处的值所决定，则称A为微分算子。

当A还是线性时，称A是线性微分算子。

位势一般位势是经典位势的一种直接推广形式，常为一个二元数值函数（核）关于某个测度的积分。

设(Ω,𝓕)是一个可测空间，K(x,y)是从Ω×Ω到[-∞,+∞]的可测函数，μ是𝓕上的实测度。若对每个x∈Ω，下式中的积分有意义，则由Ω到[-∞,+∞]的函数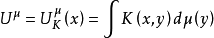称为μ以K为核的一般位势，简称位势。

本词条内容贡献者为:

杜强 - 高级工程师 - 中国科学院工程热物理研究所