[科普中国]-渐近值

渐近值是整函数的一种特定极限值。若存在一条延伸至无穷的路径 Γ ，沿着它函数 f(z) 趋于一确定的值 a ，则称 a 为 f(z) 的一渐近值， Γ 是相应于 a 的定值路径或称渐近路径。

定义定义一

渐近值是整函数的一种特定极限值。

若存在一条延伸至无穷的路径 Γ ，沿着它函数 f(z) 趋于一确定的值 a ，则称 a 为 f(z) 的一渐近值， Γ 是相应于 a 的定值路径或称渐近路径。

定义二

与函数增长速度有关的复数值。设 f 为亚纯函数，如果存在趋于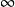的曲线 Γ ，使得当 z 沿着 Γ 趋于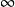时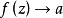，，则 a 为 f 的一个渐进值。对增长比较慢的函数，其渐近值也相应地比较少，特别地，任何有理函数至多只有一个渐进值。

发展艾弗森(Iversen,F.)于 1914 年曾证明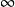，是每个非常数整函数的渐近值。

此外阿尔福斯(Ahlfors , L. V.)于 1930 年曾证明当儒瓦(Denjoy, A.)的下述猜测：有穷 P 级的整函数至多有 2ρ 个有穷渐近值。为此阿尔福斯于 1936 年获得了首届菲尔兹奖。1

整函数整函数总可以在原点展开成泰勒级数，它在全平面收敛，整函数以∞点为唯一的孤立奇点，它在∞点的罗朗展式与它在原点的泰勒展式有一样的形式。当∞点是整函数的可去奇点时，这个整函数只能是常数，这就是著名的刘维尔定理，通常表述为“有界整函数必为常数”。

本词条内容贡献者为:

王海侠 - 副教授 - 南京理工大学