[科普中国]-茹利亚方向

概念

茹利亚方向(Julia direction)是指函数值分布的奇异方向。对于超越整函数(或超越亚纯函数)，茹利亚方向是复平面C内由原点出发的具有下述性质的半射线J={z|arg z=θ0}：在以J为平分角线的任意小开度的角域内，若是整函数情形，函数取每一有穷值无穷多次，至多除去一个例外；若是亚纯函数情形，函数取每一值无穷多次，至多除去两个例外。茹利亚(Julia，G.M.)于1919—1921年应用蒙泰尔(Montel，P.A.)创立的正规族理论证明，任一超越整函数至少存在一条茹利亚方向。对于亚纯函数的情形需要对函数f(z)的增长性加上某些条件，例如满足：1

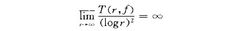
的亚纯函数存在一条茹利亚方向，其中T(r，f)是f(z)的奈望林纳特征函数。例如正负实轴是sin z的茹利亚方向。

整函数整个复平面C内的全纯函数.多项式是整函数的特殊情形.不是多项式的整函数称为超越整函数，例如：

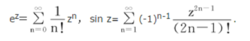
此外，两个整函数的和、差、积是整函数，又若分母恒不为零时，两个整函数的商仍为整函数。整函数可看成多项式的自然推广。代数基本定理指出，p次多项式在复平面内恰有p个根(按重数计算).据此，每一多项式有惟一的乘积表示，即：

f(z)=a(z-z1)…(z-zp)，

其中a为非零常数，z1，z2，…，zp是f(z)的零点.反之，总能构造一多项式使得它恰有事先给定的零点和相应的重级，它能表示为乘积的形式，且除去一常数因子之外是惟一确定的.此外，多项式的次数p还能给出|f(z)|增长速度的度量，即当|z|→∞时，有：

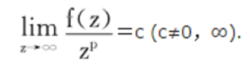
在整函数的研究中，常以多项式为模型提出并讨论相应的问题，而获得类似的结果。

整函数的一般理论源于1876年外尔斯特拉斯(Weierstrass，K.(T.W.))的工作，他的两个基本定理成为这一理论的出发点.他的第一个定理是关于整函数的因子分解的(参见“魏尔斯特拉斯第一定理”).1882-1884年，拉盖尔(Laguerre，M.)引入整函数的格这一新的概念，以此来区分整函数的类，整函数的格在某种意义下类似于多项式的次数.1883年，庞加莱(Poincaré，(J.-)H.)建立了整函数的最大模：

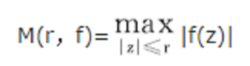
与格的一个关系，即格为k的整函数满足：

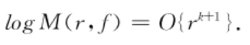
随后，1893年，阿达马(Hadamard，J.(-S.))得到一系列结果，它们合起来构成了庞加莱定理的反命题。另一方面，1897年，波莱尔(Borel，(F.-É.-J.-)É.)给出了整函数的级的一个定义。整函数f(z)的级为：

外斯特拉斯的第二个定理是关于值分布的。1879年，皮卡(Picard，(C.-)É.)用椭圆模函数的方法证明了下述重要而深刻的定理：如果一整函数f(z)不取两个有穷值，则f(z)为一常数。1896年，波莱尔给出了皮卡定理的一个初等证明.他还证明，每一个有穷ρ级的整函数，下式对所有a∈C成立：2

至多除去一个例外的a，其中n(r，a)是圆盘{z||z|≤r}内f(z)的a值点个数，并按重级计算。

20世纪的前20年，波莱尔的结果是整函数理论中最高的成就。它使皮卡定理定量化，而且波莱尔定理中考虑的是函数的a值点数而不是庞加莱定理和阿达马的结果中所考虑的零点数。这一点还显示出有穷级整函数值分布的对称性。在此意义下，它与多项式的结果是相似的。在整函数理论发展过程中，威曼(Wiman，A.)、瓦利隆(Valiron，G.)、林德勒夫(Lindelo¨f，E.L.)等人的工作也很活跃，并做出了许多贡献。20世纪20年代，奈望林纳(Nevanlinna，R.)创立了很广泛的亚纯函数值分布理论，它包括了整函数的经典结果作为其特殊情形，而且形式更为精美。

亚纯函数除极点外为全纯的函数为亚纯函数，它是复变函数论研究的主要对象之一。

德国数学家外尔斯特拉斯、瑞典数学家米塔-列夫勒、法国数学家柯西等都是亚纯函数理论的奠基人。1876年，外尔斯特拉斯证明了一个亚纯函数可以表示为两个整函数的商。第二年，瑞典数学家米塔-列夫勒推广了外尔斯特拉斯的结果，证明在任意一个区域上的亚纯函数皆可表示为两个函数的商，其中每一个都在该区域内解析。法国数学家柯西也曾给出一种分解方法，对相当广的一类亚纯函数得到简单的表示式。

近代亚纯函数理论是20世纪20年代由芬兰数学家奈望林纳所创立。他在1925年发表了亚纯函数的一个一般性理论，这个理论中有两个基本定理分别被称为第一基本定理和第二基本定理，从它们可以推出一系列关于亚纯函数的值分布的结果，丰富并推进了前人的工作，产生了深远影响。

亚纯函数的术语是由法国数学家布里奥和布凯共同引进的。

人物简介——蒙泰尔法国数学家。生于尼斯(Nice)。巴黎大学教授。1937年被选为巴黎科学院院士。主要贡献在解析函数论和拓扑学方面。在解析函数论中、他引进了“正规函数族”的概念，给出了解析函数族是正规族的条件的“蒙泰尔定理”。主要著作有《正规解析函数族及其应用》(Lecons sur lesfamilles normales de fonctions analytiques et leurs applications，1927)和《单叶和多叶函数》(Lec-ons sur les fonctions univalentesou multivalentes，1933)。在线性拓扑空间中。他建立了所谓蒙特尔空间，简称(M)—空间。根据他的贡献，法国许多大学和其它国家的一些大学都授予他荣誉博士称号。3