[科普中国]-波莱尔例外值

基本介绍

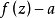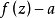波莱尔例外值(exceptional value of Borel)是整函数亚纯函数理论的一个概念，使的零点的收敛指数小于函数的级的值a称为波莱尔例外值。它亦能叙述为下面的形式：设是在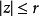内的零点数(按重级计算)，若

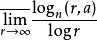小于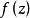的级ρ，则称为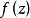的波莱尔例外值，波莱尔定理断言，对于整函数至多有一个波莱尔例外值，对亚纯函数至多有两个波莱尔例外值1。

波莱尔定理波莱尔定理(Borel theorem)是关于整函数值分布的重要定理，1897年为波莱尔(Borel，(F.-É.-J.-)É.)所证明。定理叙述如下：设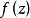是有穷ρ级整函数，则对一切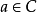都有

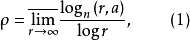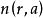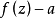至多可能除去一个例外值a，式中是在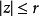内之零点个数(按重级计算)。此定理大大推进了皮卡定理，因为根据皮卡定理只知道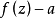有无穷多个根，但并不知道其稠密程度。波莱尔定理显示了有穷级整函数值分布的对称性，即除去可能有一个a值以外，所有的a值点数能由函数的增长速度来确定。关于亚纯函数的波莱尔定理可叙述如下：设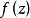是有穷ρ级的亚纯函数，则对一切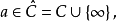都有(1)式成立，至多可能除去两个例外的a1。