[科普中国]-诺伊曼问题

人物介绍

卡尔·戈特弗里德·诺依曼（也是卡尔; 1832年5月7日 - 1925年3月27日）是德国数学家。2

诺伊曼出生于普鲁士的科尼斯堡，是科尼斯堡大学矿物学家，物理学家和数学家弗朗茨·恩斯特·诺伊曼（Franz Ernst Neumann）（1798-1895）的矿物学和物理学教授。卡尔·诺依曼（Carl Neumann）在科尼斯堡（Hönigsberg）和哈雷（Halle）学习，并曾在哈雷，巴塞尔，杜宾根和莱比锡的大学担任教授。

在科尼斯堡，他和父亲一起学习物理学，后来作为一名工作的数学家，几乎完全处理了物理学的问题。 诺伊曼受到黎曼的电动力学研究的推动，发明了一种基于电动力学有限传播的理论，感兴趣的是威廉·爱德华·韦伯和鲁道夫·克劳修斯，他与他进行了通信。韦伯描述了纽曼在莱比锡的教授，他说：“更高的力学，基本上包括数学物理学”，他的讲座是这样做的[1]麦克斯韦提到了韦伯和诺依曼在“电磁场动力学理论导论”（1864）中开发的电动理论。

诺伊曼从事狄利克雷定理，可以被认为是积分方程理论的发起者之一。诺伊曼级数，类似于几何级数：

对无限矩阵的条件下的原理是以他命名而来的。

与Alfred Clebsch Neumann一起创立了数学研究杂志Mathematische Annalen。他死在莱比锡。

某些类型的普通和偏微分方程的诺伊曼边界条件以他命名。3

调和函数在区域上满足拉普拉斯方程的多元函数.设F(x1，x2，…，xn)是定义在区域D⊂R上的具有二阶连续偏导数的函数，且F在区域D上满足下述的拉普拉斯方程：

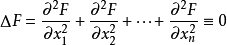则称F是区域D上的调和函数，或者说F在区域D上是调和的。称：

为拉普拉斯算子。一个复值函数的实部与虚部都是在区域D上调和的，有时也称它是区域D上的(复值)调和函数。如果F(z)=F(x+iy)是复变量z=x+iy的解析函数(在复平面的某个开集内)，那么F的实部u和虚部v作为(x，y)的二元实函数都是调和函数，它们满足所谓的柯西-黎曼方程：

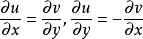这样的一对调和函数称为是彼此共轭的。当n≥2时，若u1，u2，…，un都是区域D⊂R上的调和函数，且满足下述偏微分方程组：

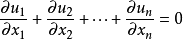
则称(u1，u2，…，un)是区域D上的一个共轭调和函数系。调和函数与傅里叶级数的关系密切。

定义诺伊曼问题(Neumann problem)亦称第二边值问题。调和函数的一类重要边值问题。设在区域D的边界∂D上给定了一个连续函数φ(z)，在D内求一个调和函数u(z)，要求它具有连续到边界的一阶偏导数，且在∂D上的外法向导数∂u/∂n等于φ(z).对于给定的D及其边界上的给定函数φ(z)，若满足要求的u(z)存在，则可以相差一个实常数。

对二阶椭圆型方程求边界上的法向导数为已知的解。设Ω为R中的有界域，它的边界由有限个光滑曲面Γ所构成.对于偏微分方程：

求在闭域Ω上连续、在Ω的边界Γ上满足条件：

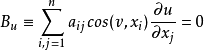
的解的问题称为诺伊曼问题或者第二边值问题。如果c(x)