[科普中国]-光滑映射在一点稳定性

概念

光滑映射在一点稳定性(stability of asmooth mapping at a point)是指光滑映射在一点局部经小扰动后本质不变的特性。设Mm，Nn是两个微分流形，p∈Mm，q=f(p)，f：U→Nn是光滑映射，U是点p的邻域。若对于任何足够接近于映射f的映射f~：U→Nn，都存在点p和点q的邻域V和W，p∈V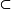 U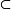 Mm，q∈W 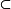Nn和微分同胚嵌入h：V→U，k：W→Nn，使得有如下（图1）交换：1

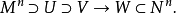
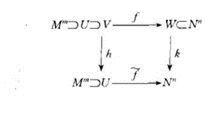
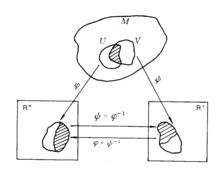
光滑映射一类连续映射，是微分拓扑学的基本概念和主要研究对象。它是微分流形之间在每点附近的局部表示。设M，N分别是m维，n维微分流形，f：M→N是连续映射，对于p∈M，(U，φ)，(V，ψ)分别是M含p的卡及N含f(p)的卡，f(U)V，则映射：

称为f关于卡(U，φ)，(V，ψ)的局部表示，它是Rm中的开集φ(U)到Rn中的开集ψ(V)的连续映射。连续映射f：M→N，若对于p∈M，f(p)∈N，存在卡(U，φ)，卡(V，ψ)与f(U)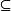 V，使得f的局部表示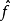是C可微的(见图2)，则称f在p∈M处是C可微的。连续映射f：M→N，若f在每点p∈M处都是C可微的，则称f为Cr可微映射。此时，简称f为C∞映射。M到N的C∞映射称为M到N的光滑映射。2

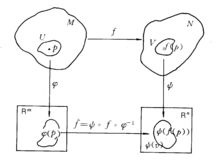
微分流形设M是仿紧豪斯道夫 (Hau-sdorff)空间，且是拓扑流形，称A= {(Uα，Фα)|α∈P}是它的地图，如果{Uα|α∈P}是M的开覆盖，Фα是从Uα到n维欧氏空间R的某开集上的同胚。(Uα，Φα)称为坐标卡。如果两个坐标卡 (Uα，Фα)，(Uβ，Φβ) 满足Uα∩Uβ≠Φ，则称Φβ·Фα：Φα(Uα∩Uβ) →Φβ(Uα∩Uβ) 和Φα·Φβ： Φβ(Uα∩Uβ) →Фα(Uα∩Uβ) 为Uα∩Uβ上的坐标变换。如果A的所有坐标变换都是C可微的，则称A为一个C地图，其中1≤r≤∞。r也可等于ω，此时A称为解析地图。拓扑流形M的坐标卡 (U，Φ) 称为与A是Cr相容的，如果任意(Uα，Φα) ∈A，坐标变换Φ·ΦαΦα·Φ均C可微。拓扑流形M的C地图A称为最大的，如果它包含M的所有与之C相容的坐标卡。M上的最大C地图A称为M的C微分结构。(M，A)称为C微分流形，或简称为C流形。当r=∞时，C微分结构也称为光滑结构，C流形也称为光滑流形。r=ω时，C结构也称为解析结构，C流形称为解析流形。C流形(M，A)有时也简记为M。

从直观上看，拓扑流形是局部欧氏空间，局部之间用同胚映射(坐标变换)粘贴在一起。n维C流形，不仅局部同胚于n维欧氏空间，而且局部之间是用C光滑、且其逆也C光滑的坐标变换粘贴在一起。

两个C流形M和N，f：M→N是连续映射，且任一点P∈M，有包含P点的M中的坐标卡(U，Φ)以及包含f(P)的N中的坐标卡(V，)，使得f(U)⊂V，同时，映射°f°Φ-1：Φ(U)→(V)是C光滑的(1≤r≤∞或r=ω)，则称f是C映射。C映射也称为光滑映射，C映射也称为解析映射。

C流形M和N之间的同胚f：M→N，如果f和f均是C映射，则称f是C微分同胚。

微分同胚微分流形之间的一类同胚映射。它与它的逆映射都是可微的。设M，N均为微分流形，对于映射f：M→N，若f是同胚映射，并且f，f都是C可微映射，则称f为M到N上的C微分同胚。C微分同胚f：M→N简称M到N上的微分同胚。对于微分流形M，N，若存在(C)微分同胚f：M→N，则称M与N是(C)微分同胚的微分流形，记为M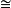 N。“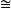 ”是微分拓扑学中的基本等价关系。微分拓扑的基本任务是研究微分流形在微分同胚下保持不变的性质，以及寻求在怎样的条件下两个微分流形是微分同胚的。米尔诺(Milnor，J.W.)于1956年证明，在S7上至少存在两个不微分同胚的微分构造。后来证实，S7上恰好有15个这样的不同的微分构造。3

微分拓扑学研究微分流形和可微映射的一个数学分支。1936年由美国数学家惠特尼开创。惠特尼证明了微分流形的嵌入定理，还研究了n维流形的可微结构。另一位美国数学家S.S.凯恩斯同期证明了三角形剖分定理、微分流形的可单形剖分性等结果。1940年英国数学家J.H.C.怀特海得到组合流形的正则邻域定理，他还第一次给出了整体微分流形概念的严格而精确的定义。20世纪50年代初，法国数学家托姆创立配边理论，完成多维流形的粗分类工作。1958年美国数学家米尔诺出版《微分拓扑学》，其中有许多该学科的重要成果。20世纪60年代初，美国数学家斯梅尔证明了微分拓扑学中最重要的定理之一——广义庞加莱猜想，即维数n≥5时庞加莱猜想成立，为此荣获1965年的维布伦奖和1966年的菲尔兹奖。同时期的凯瓦雷、塞曼、马祖尔等人亦在微分流形研究中得到许多结果。微分拓扑学还集中研究微分映射的性质、组合结构与微分结构之间的关系、组合流形的光滑化问题、嵌入问题等，它在20世纪60年代取得较大发展。近一二十年来，微分拓扑学仍在微分浸入、微分嵌入、配边等理论方面不断发展。例如美国数学家M.弗里德曼利用拓扑流形的剜补术于1981年证明了4维的庞加莱猜想，并因此引起关于4维流形拓扑的一系列研究。4