[科普中国]-赛费特纤维空间

赛费特纤维空间(Seifert fibre spaces)亦称赛费特流形。一类特殊的3维流形。除了3维球面与透镜空间以外，赛费特纤维空间是一类较为具体，研究得较多的3维流形，而且它在3维流形上的齐性几何(即常曲率几何)中扮演着重要的角色。1

简介赛费特纤维空间(Seifert fibre spaces)亦称赛费特流形。一类特殊的3维流形。除了3维球面与透镜空间以外，赛费特纤维空间是一类较为具体，研究得较多的3维流形，而且它在3维流形上的齐性几何(即常曲率几何)中扮演着重要的角色。一个3维流形M，若它能表示为M中一些互不相交的简单闭曲线之并，则称为赛费特纤维空间，这些闭曲线称为M的纤维。1

详细释义若对于其中的一个纤维c，取c在M中的正则邻域N(c)，可以要求N(c)由M中的一些纤维所构成，则把N(c)看做独立于M之外的流形，有N(c)=B×S，而当N(c)按原来的方式放回到M时，对于N(c)上的一个纤维c′，在B×S上可以表示为λμ，其中λ代表π1(B×S)中的生成元S，μ代表其中的生成元B.当n=±1时，称c为正则的，否则c称为奇异2的。由于在奇异纤维附近的纤维都是正则的，当M为紧致流形时，M中仅有有限个奇异纤维，M为正则纤维之并。现在对M的研究，可着眼于这些奇异纤维上，通过适当调整c′的取向，总可假定n>0，0≤m≤n/2。若将M中每条纤维等同为一个点，则得轨道空间S，以及射影η：M→S。由于η(N(c))为S中的一个2维胞腔，从而表明S为2维流形，称为M的伴随赛费特曲面。设M有奇异纤维cα1，cα2，…，cαq，B1，B2，…，Bq为η(cα1)，η(cα2)，…，η(cαq)在S中互不相交的2维胞腔邻域。若S=S-∪Int Bi， M=η(S)，则η|M：M→S为通常意义下的纤维丛映射。若S≠0(当M无奇异纤维时，把一个正则纤维看做奇异即可)，则S可收缩为圆周的一点并，因此η|M：M→S有截面，选η(Bi)的生成元ci，ti，其中ti为M上正则纤维，ci与ti相交于一点。另一方面，已有η(Bi)的生成元μi，λi，而ti=μiλi(当cαi为(mi，ni)型奇异纤维时)，所以ci=μiλi，其中simi-rini=1， μi=tici，这样可以由π1(M)中增加关系tici=1而计算π1(M)。具体说来，由范卡彭定理易知有下列结果：若M为有g个奇异纤维的赛费特纤维空间，其赛费特曲面S有亏格g以及k个边界分支。

若赛费特纤维空间M为闭流形，则其中的赛费特结构可能不惟一，但是它上面的齐性几何由两个不变量决定，其一为赛费特曲面S的欧拉示性数χ，其二为M的欧拉示性数e。

3维流形的几何研究3维流形上的常曲率几何。至今可以用三种方式来谈论几何，第一种：古典的欧氏几何，在其中考虑点、线、面、角、长度等以及它们之间的相互关系，而且这种方法对于非欧几何也适用；第二种：微分几何;第三种是克莱因意义下的几何，即考虑空间X与其上的—个可迁变换群G，所谓几何(X，G)即考虑X在G之下的那些不变性.当然这三者只是立论不同而已，其内容有时是共通的。在这里所论的几何正是克莱因意义之下的几何。由于流形M与它的泛覆叠空间X之间有相同的度量，所以为了讨论流形M上的局部齐性度量，只须讨论X上的齐性完备度量即可，其中G=Isom(X)，即X上的保距群，并假定G有子群H，使得轨道空间(流形)X/H是紧致的(称为(X，G)有紧商).在这些限制之下，瑟斯顿(Thurston，W.P.)有下列定理：

1.任何单连通3维流形X上有紧商的完备齐性几何(X，Isom(X))等价于下列8种几何之一：

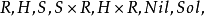(此处X~表示X的覆叠空间)，其中R为3维欧氏空间，H，H分别为2维与3维双曲空间，S，S上有分别作为R，R的子空间的诱导几何。

2.任何闭3维流形上，若有模型于上述意义下的几何，则这种几何是惟一的。

当然，瑟斯顿也注意到在闭3维流形的非平凡连通和之中，除了RP#RP以外，均无上述意义下的几何，因此他的工作中也包含一些几何猜想，即他认为任何紧致、可定向3维流形，当用其中一些互不相交的球面与环面去切，并在球面的切口处再补上3维球体以后，必然有几何结构。这些猜测之中包含着著名的庞加莱猜想，但是看来要证实它们还须走漫长的道路.在3维流形上存在常曲率几何，这是近年来由瑟斯顿发展起来的一个新的研究课题，它对于流形性质的研究具有重要的意义。

透镜空间透镜空间是一类特殊的可定向闭3维流形。有了3维闭流形的海嘎特分解与海嘎特图概念以后，一个有趣的问题是，能否对于有某一固定亏格的海嘎特图的流形进行分类。当亏格为1时，即对于分解(V，V′)，其中V=V′为环面或克莱因瓶，赖德迈斯特(Reidemeister，K.W.F.)于1935年成功地进行了分类，所得到的闭3维流形是透镜空间或S上的不可定向S丛。但是，对于亏格大于1的情形，至今尚无相应的结果。若V=S×B为环体，π1(V)是环面V的基本群，以S=a以及B=b为生成元，则V上的闭曲线ab为简单闭曲线当且仅当p，q互素.于是，给定整数p，q，使得p≥0，(p，q)=1，则存在惟一3维闭流形Lp，q，它由海嘎特图(V;J)决定，并且J为V上的简单闭曲线，它在π1(V)中表示的元素为ab，这种流形称为p，q型的透镜空间。3

本词条内容贡献者为:

王海侠 - 副教授 - 南京理工大学