[科普中国]-剩余类环

定义

设A是环R的一个理想，若把A，R看作加群，这样A是R的一个不变子群，且由A的陪集a+A=[a]，b+ A=[b],..作成R的一个分类，这些类叫做模A的剩余类。而所有这些类组成的集作成一个环，叫做模A的剩余类环，记作R/A。

比如，(n)是Z的一个理想，由(n)的陪集0+(n)=[0]，1+(n)=[1]，2+(n)=[2]，...，n-1+(n)= [n-1]作成Z的一个分类，且集合{[0]，[1],...,[n-1]}作成一个剩余类环Z/(n),也就是Zn。可见，一般的剩余类环是模n的剩余类环Zn的推广2。

实例分析现在我们将给出剩余类环这个重要概念的另一个实例。令F是一个实数域，并且考虑环F[x]中的理想n= (x2+1)，如果f(x)是F[x] 的任意元素，那么由除法变换我们有：f(x)=g(x)(x2+1)+a+bx，此处a和b都是实数，因此，对模n的每一个剩余类所包含的是零或者至多是一次的多项式，而且a+bx和c+dx在不同的剩余类中，除非是a=c和b=d，因为除了在这种情况下，a+bx≡c+dx(n)是不可能的，这样F[x}/n的不同元素的确就是剩余类

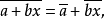由F[x]/n中加法和乘法的定义，我们看到

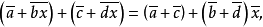和

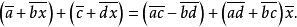上面的第一式是明显的，而第二式由观察式：(a+bx)(c+dx)=ac-bd+(ad+bc)x+bd(x2+1)，所以(a+bx)(c+dx)=(ac-bd)+(ad+bc)x(n)，读者必须注意这些公式与复数的加法和乘法的普通规则的相似性——事实上，环F[x]/(x2+ 1) 就是复数域，除了使用的符号以外，实质上是相同的。

另外一个实例可能是有趣的，令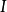是一个整数环，而m是多项式环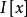中的理想(2，x2+x+1)，利用前面例子的论证，以x2+x+1代替x2+1，可以看出，对模m的任一个剩余类包含一个形如a+bx的元素，现在此处a和b都是整数，然而在这种情况下，m包含整数2，因而每一个整数对模m的同余不是0就是1，因此刚好有4个剩余类，就是

而且因为x(x+1)=1+(x2+x+1)-2≡1(m)，我们看到

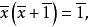所以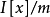的每一个非零元素有一个逆元，因此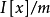是一个域，这就是我们的第一个有限域的实例，它不是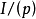的形式，此处p是一个素数，事实上，可以证明，虽然我们省略这个证明，那就是对于适当选择的理想m，则任何有限域都可以象剩余类环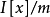一样而得到3。

相关定理定理1**(环同态基本定理)**设A是环R的一个理想，则R~R/A；反之，设环R与环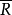同态，则同态映射的核A是R的一个理想，且。

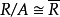比如，整数环Z与模n的剩余类环Zn同态，即Z~Zn；反之，如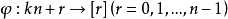是Z到Zn的同态满射，即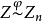，且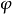的核A=(n)，所以。

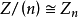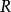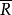定理2若环~环，则

①R的一个子环S的象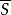是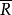的一个子环；

②R的一个理想A的象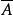是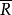的一个理想；

③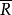的一个子环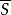的逆象S是R的一个子环；

④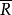的一个理想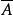的逆象A是R的一个理想2。