[科普中国]-分歧群

概念介绍

分歧群(ramification group)是惯性群的一个正规子群。它所决定的商群同构于某个有关的特征标群。设N是域F的一个正规扩张，C与π，N-分别是N的一个赋值环与对应的位、剩余域，Δ，Γ分别是赋值环C，C∩F的(加法)值群.若φ是与C对应的赋值，则φ诱导一个从N·到Δ/Γ的群同态映射w，使得：2

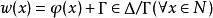若Ω是N-的代数闭包，且HΩ(Δ/Γ)是商群Δ/Γ到Ω内的特征标群，则存在一个从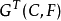到HΩ(Δ/Γ)的满同态ψ，使得对任意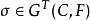，有：

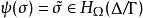
当且仅当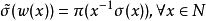。同态映射ψ的核称为C关于F的分歧群，记为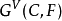。分歧群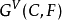的构造可按如下方式给出：

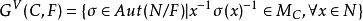
其中MC为C的赋值理想。分歧群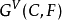在N中的固定子域称为C关于F的分歧域。3

群群是一种只有一个运算的、比较简单的代数结构;是可用来建立许多其他代数系统的一种基本结构。

设G为一个非空集合，a、b、c为它的任意元素。如果对G所定义的一种代数运算“·”(称为“乘法”，运算结果称为“乘积”)满足：

(1)封闭性，a·b∈G;

(2)结合律，即(a·b)c = a·(b·c);

(3)对G中任意元素a、b，在G中存在惟一的元素x，y，使得a·x= b，y·a=b，则称G对于所定义的运算“·”构成一个群。例如，所有不等于零的实数，关于通常的乘法构成一个群;时针转动(关于模12加法)，构成一个群。

满足交换律的群，称为交换群。

群是数学最重要的概念之一，已渗透到现代数学的所有分支及其他学科中。凡是涉及对称，就存在群。例如，可以用研究图形在变换群下保持不变的性质，来定义各种几何学，即利用变换群对几何学进行分类。可以说，不了解群，就不可能理解现代数学。

1770年，拉格朗日在讨论代数方程根之间的置换时，首先引入群的概念，而它的名称，是伽罗华在1830年首先提出的。

惯性群惯性群是群表示论中一类重要的群。可由正规子群特征标的稳定子群决定的群。设N是一个有限群G的正规子群，θ是N的一个特征标，G的元g如下地作用在θ上：对每a∈N使θ(a)=θ(gag)，这时θ仍是N的特征标，将θ的稳定子群IG(θ)={g∈G|θ=θ}称为θ的惯性群。

设R是一个交换环，W是一个右RN模。对任意g∈G，做一个右RN模记为gW如下：它作为R模与Wg同构。对w∈W，记它在Wg中的对应元为wg。于是Wg={wg|w∈W}。任意a∈N，若a对Wg中元wg的作用为wga=(w(gag^-1))g，则IG(W)={g∈G|WW}称为RN模W的惯性群。当R是域时，若W提供的特征标为θ，则W提供的特征标正是θg。这时IG(θ)=IG(W)。4

正规子群正规子群亦称不变子群。一类重要的子群。在共轭作用下不变的子群。设H是群G的一个子群，若对任意的x∈G有Hx=xH，则称H是G的一个正规子群，记为HG。子群H是G的正规子群的充分必要条件是对于任意的h∈H，x∈G，有xhx∈H.{e}和G是G的两个正规子群，称为G的平凡正规子群。

同构两个数学系统(例如两个代数系统)，当它们的元素及各自所定义的运算一一对应，并且运算结果也保持一一对应，则称这两个系统同构，记为≌。它们对于所定义的运算，具有相同的结构。例如，十进制数与二进制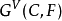数是同构的。

建立同构关系的映射，称为同构映射。例如，当映射为一一映射，并且对应元素关于运算保持对应时，就是同构映射。

同构是数学中最重要的概念之一。在很多情况，一个难题往往可以化成另一个同构的、似乎与它不相关的、已经解决的问题，从而使原问题方便地得到解决。虽然数学发展得越来越复杂，但利用同构概念，不仅使数学得到简化，而且使数学变得越来越统一。表面上似乎不同，但本质上等价的结果，可以用统一的形式表达出来。例如，如果四色定理得到了证明，其他数学分支中与它同构的几十个假设，也同时得到了证明。5