全分歧扩张(totally ramified extension)是一类有限赋值域扩张,它是与非分歧扩张相反的概念。赋值域(F,B)的一个有限扩张(K,C),若分歧指数e(C|F)=[K∶F],则称此扩张为全分歧扩张。此时,B对于K是无亏损的,且C是B在K上的惟一拓展1。
定义设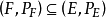 是完备离散赋值域的有限扩张,以
是完备离散赋值域的有限扩张,以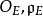 表示E的赋值环和素理想,
表示E的赋值环和素理想,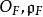 表示F的赋值环和素理想,而
表示F的赋值环和素理想,而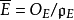 和
和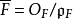 分别表示E和F的剩余类域。令
分别表示E和F的剩余类域。令 ,则
,则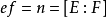 。如果
。如果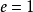 (从而
(从而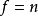 ),称
),称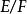 为不分歧扩张。如果
为不分歧扩张。如果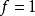 (从而
(从而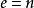 ),称
),称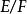 为完全分歧扩张(或纯分歧扩张)。
为完全分歧扩张(或纯分歧扩张)。
完全分歧扩张的刻画首先回忆
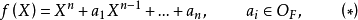 称为Eisenstein多项式是指
称为Eisenstein多项式是指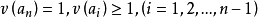 .
.
定理1设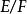 是完备离散赋值域的有限扩张,
是完备离散赋值域的有限扩张,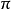 是E的一个素元。
是E的一个素元。
(1)若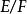 是完全分歧的,则
是完全分歧的,则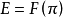 ,并且
,并且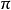 在F上的最小多项式为Eisenstein多项式。
在F上的最小多项式为Eisenstein多项式。
(2)反之,若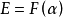 ,并且
,并且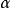 在F上的最小多项式是Eisenstein多项式,则
在F上的最小多项式是Eisenstein多项式,则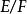 是完全分歧扩张,并且
是完全分歧扩张,并且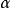 是E的一个素元。
是E的一个素元。
定理2设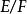 为n次扩张且
为n次扩张且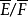 可分,则存在中间域
可分,则存在中间域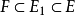 使
使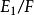 为非分歧扩张,
为非分歧扩张,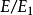 为完全分歧扩张;且有单位
为完全分歧扩张;且有单位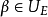 使
使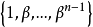 为
为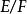 的整基。
的整基。
例1当p为奇素数时,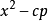 和
和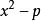 均是Eisenstein多项式
均是Eisenstein多项式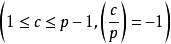 ,所以
,所以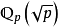 和
和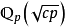 都是
都是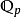 的完全分歧扩张。对于p=2,同样可知
的完全分歧扩张。对于p=2,同样可知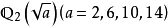 是
是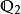 的完全分歧扩张,进而对
的完全分歧扩张,进而对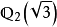 和
和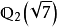 ,我们有
,我们有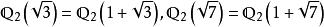 ,而
,而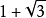 和
和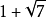 在
在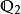 上的极小多项式
上的极小多项式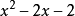 和
和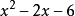 都是对
都是对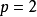 的Eisenstein多项式,所以
的Eisenstein多项式,所以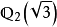 和
和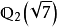 也是
也是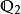 的完全分歧扩张2。
的完全分歧扩张2。
不分歧扩张的刻画定理3(1)设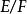 是不分歧扩张,如果
是不分歧扩张,如果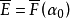 ,取元素
,取元素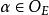 ,使得
,使得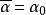 ,则
,则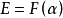 ,并且若
,并且若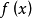 是
是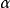 在F上的极小多项式,则
在F上的极小多项式,则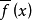 是
是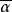 在F上的极小多项式。
在F上的极小多项式。
(2)若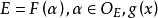 是
是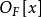 中首1多项式,
中首1多项式,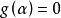 。如果
。如果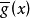 (在
(在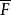 的代数闭包
的代数闭包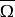 中)没有重根,则
中)没有重根,则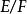 是不分歧扩张。
是不分歧扩张。
引理设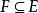 是完备离散赋值域的有限扩张,并且
是完备离散赋值域的有限扩张,并且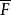 是有限域。
是有限域。
(1)对于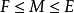 ,则
,则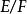 不分歧当且仅当
不分歧当且仅当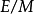 和
和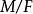 均不分歧。
均不分歧。
(2)若 是有限扩张,
是有限扩张,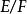 不分歧,则
不分歧,则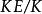 不分歧。
不分歧。
(3)若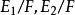 均不分歧,则
均不分歧,则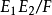 不分歧。
不分歧。
定理4(1)设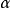 是
是 中的
中的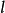 次本原单位根,并且
次本原单位根,并且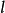 与p互素,以n表示满足
与p互素,以n表示满足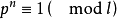 的最小正整数,则
的最小正整数,则 是
是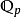 的n次不分歧扩张,并且这是伽罗瓦扩张,其伽罗瓦群
的n次不分歧扩张,并且这是伽罗瓦扩张,其伽罗瓦群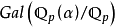 是由自同构
是由自同构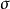 生成的n次循环群,其中
生成的n次循环群,其中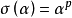 。
。
(2)对每个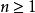 ,
,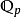 都存在惟一的n次不分歧扩张。
都存在惟一的n次不分歧扩张。
(3)设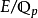 是有限扩张,则存在中间域F,使得
是有限扩张,则存在中间域F,使得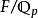 为不分歧,而
为不分歧,而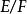 是完全分歧2。
是完全分歧2。
本词条内容贡献者为:
王海侠 - 副教授 - 南京理工大学




 扫码下载APP
扫码下载APP

 科普中国APP
科普中国APP
 科普中国
科普中国
 科普中国
科普中国