[科普中国]-商赋范线性空间

商赋范线性空间是由赋范线性空间与其闭子空间诱导出的新的赋范线性空间。

简介商赋范线性空间是由赋范线性空间与其闭子空间诱导出的新的赋范线性空间。

设E是赋范线性空间(X,||·||)的闭线性子空间，对于商空间X/E中每个元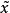，规定范数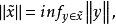则X/E成为赋范线性空间，称为商赋范线性空间，这个范数称为原来范数的诱导范数。

性质如果(X,||·||)是巴拿赫空间，则商空间X/E按诱导范数也是巴拿赫空间。1

赋范线性空间赋范线性空间(normed linear space)是在线性空间中引进一种与代数运算相联系的度量，即由向量范数诱导出的度量。赋范线性空间称为Banach空间，是指由范数导出的度量是完备的。

定义：设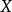是线性空间，函数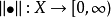称为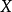上定义的一个范数，如果满足：

（1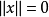）当且仅当；

（2）对任何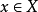及，；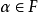

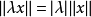（3）对任意，。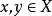

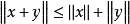称二元体为赋范线性空间。

本词条内容贡献者为:

李嘉骞 - 博士 - 同济大学